Advertisements
Advertisements
प्रश्न
What is the ratio in which the line segment joining (2, -3) and (5, 6) is divided by x-axis?
पर्याय
1:2
2:1
2:5
5:2
उत्तर
1:2
Explanation:
Let the line joining points A (2, -3) and B (5, 6) be divided by point P (x, 0) in the ratio k:1.
y = `(ky_2 + y_1)/(k + 1)`
0 = `(k xx 6 + 1 xx (-3))/(k + 1)`
0 = 6k – 3
k = `1/2`
Thus, the required ratio is 1:2.
APPEARS IN
संबंधित प्रश्न
If A(–2, –1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram, find the values of a and b
If the coordinates of the mid-points of the sides of a triangle are (1, 2) (0, –1) and (2, 1). Find the coordinates of its vertices.
In what ratio does the point `(24/11, y)` divide the line segment joining the points P(2, –2) and Q(3, 7)? Also find the value of y.
Find the ratio in which the join of (–4, 7) and (3, 0) is divided by the y-axis. Also, find the co-ordinates of the point of intersection.
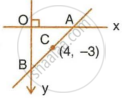
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
If the point C (–1, 2) divides internally the line-segment joining the points A (2, 5) and B (x, y) in the ratio 3 : 4, find the value of x2 + y2 ?
In what ratio is the line joining (2, -1) and (-5, 6) divided by the y axis ?
Point P(– 4, 6) divides point A(– 6, 10) and B(m, n) in the ratio 2:1, then find the coordinates of point B
Complete the following activity to find the coordinates of point P which divides seg AB in the ratio 3:1 where A(4, – 3) and B(8, 5).
Activity:
∴ By section formula,
∴ x = `("m"x_2 + "n"x_1)/square`,
∴ x = `(3 xx 8 + 1 xx 4)/(3 + 1)`,
= `(square + 4)/4`,
∴ x = `square`,
∴ y = `square/("m" + "n")`
∴ y = `(3 xx 5 + 1 xx (-3))/(3 + 1)`
= `(square - 3)/4`
∴ y = `square`
A line intersects y-axis and x-axis at point P and Q, respectively. If R(2, 5) is the mid-point of line segment PQ, them find the coordinates of P and Q.
