Advertisements
Advertisements
प्रश्न
What is the ratio in which the line segment joining (2, -3) and (5, 6) is divided by x-axis?
विकल्प
1:2
2:1
2:5
5:2
उत्तर
1:2
Explanation:
Let the line joining points A (2, -3) and B (5, 6) be divided by point P (x, 0) in the ratio k:1.
y = `(ky_2 + y_1)/(k + 1)`
0 = `(k xx 6 + 1 xx (-3))/(k + 1)`
0 = 6k – 3
k = `1/2`
Thus, the required ratio is 1:2.
APPEARS IN
संबंधित प्रश्न
If the point C (–1, 2) divides internally the line segment joining A (2, 5) and B in ratio 3 : 4, find the coordinates of B
Prove that the points (–2, –1), (1, 0), (4, 3) and (1, 2) are the vertices of a parallelogram. Is it a rectangle ?
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Find the lengths of the medians of a ΔABC having vertices at A(5, 1), B(1, 5), and C(-3, -1).
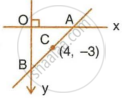
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
- Write down the co-ordinates of the point P that divides the line joining A(−4, 1) and B(17, 10) in the ratio 1 : 2.
- Calculate the distance OP, where O is the origin.
- In what ratio does the y-axis divide the line AB?
Find the ratio in which the point R ( 1, 5) divides the line segment joining the points S (-2, -1) and T (5, 13).
The perpendicular bisector of the line segment joining the points A(1, 5) and B(4, 6) cuts the y-axis at ______.
A line intersects the y-axis and x-axis at the points P and Q, respectively. If (2, –5) is the mid-point of PQ, then the coordinates of P and Q are, respectively ______.
