Advertisements
Advertisements
प्रश्न
A line intersects the y-axis and x-axis at the points P and Q, respectively. If (2, –5) is the mid-point of PQ, then the coordinates of P and Q are, respectively ______.
विकल्प
(0, – 5) and (2, 0)
(0, 10) and (– 4, 0)
(0, 4) and (– 10, 0)
(0, – 10) and (4, 0)
उत्तर
A line intersects the y-axis and x-axis at the points P and Q, respectively. If (2, –5) is the mid-point of PQ, then the coordinates of P and Q are, respectively (0, – 10) and (4, 0).
Explanation:
Let the coordinates of P and 0 (0, y) and (x, 0), respectively.
So, the mid-point of P(0, y) and Q(x, 0) is `M((0 + x)/2, (y + 0)/2)` ...`[∵ "Mid-point of a line segment having points" (x_1, y_1) "and" (x_2, y_2) = ((x_1 + x_2)/2, (y_1 + y_2)/2)]`
But it is given that, mid-point of PQ is (2, –5).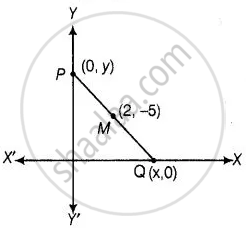
∴ 2 = `(x + 0)/2`
And – 5 = `(y + 0)/2`
⇒ 4 = x and – 10 = y
⇒ x = 4 and y = – 10
So, the coordinates of P and Q are (0, – 10) and (4, 0).
APPEARS IN
संबंधित प्रश्न
If the point C (–1, 2) divides internally the line segment joining A (2, 5) and B in ratio 3 : 4, find the coordinates of B
A point P divides the line segment joining the points A(3, -5) and B(-4, 8) such that `(AP)/(PB) = k/1`. If P lies on the line x + y = 0, then find the value of k.
If two adjacent vertices of a parallelogram are (3, 2) and (−1, 0) and the diagonals intersect at (2, −5), then find the coordinates of the other two vertices.
In Figure 2, P (5, −3) and Q (3, y) are the points of trisection of the line segment joining A (7, −2) and B (1, −5). Then y equals

M and N are two points on the X axis and Y axis respectively. P (3, 2) divides the line segment MN in the ratio 2 : 3.
Find:
(i) the coordinates of M and N
(ii) slope of the line MN.
Q is a point on the line segment AB. The coordinates of A and B are (2, 7) and (7, 12) along the line AB so that AQ = 4BQ. Find the coordinates of Q.
A (2, 5), B (-1, 2) and C (5, 8) are the vertices of triangle ABC. Point P and Q lie on AB and AC respectively, such that AP: PB = AQ: QC = 1: 2. Calculate the coordinates of P and Q. Also, show that 3PQ = BC.
Show that the line segment joining the points (-3, 10) and (6, -5) is trisected by the coordinates axis.
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P (- 3, 4) on AB divides it in the ratio 2 : 3. Find the coordinates of A and B.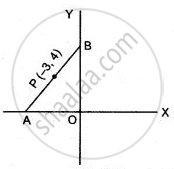
The point Q divides segment joining A(3, 5) and B(7, 9) in the ratio 2 : 3. Find the X-coordinate of Q
