Advertisements
Advertisements
प्रश्न
If two adjacent vertices of a parallelogram are (3, 2) and (−1, 0) and the diagonals intersect at (2, −5), then find the coordinates of the other two vertices.
उत्तर
Let ABCD be the parallelogram with two adjacent vertices A(3, 2) and B(−1, 0). Suppose O(2, −5) be the point of intersection of the diagonals AC and BD.
Let C(x1, y1) and D(x2, y2) be the coordinates of the other vertices of the parallelogram.
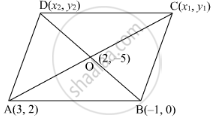
We know that the diagonals of the parallelogram bisect each other. Therefore, O is the mid-point of AC and BD.
Using the mid-point formula, we have
\[\left( \frac{x_1 + 3}{2}, \frac{y_1 + 2}{2} \right) = \left( 2, - 5 \right)\]
\[ \Rightarrow \frac{x_1 + 3}{2} = 2\ and\ \frac{y_1 + 2}{2} = - 5\]
\[ \Rightarrow x_1 + 3 = 4\ and\ y_1 + 2 = - 10\]
\[ \Rightarrow x_1 = 4 - 3 = 1\ and\ y_1 = - 10 - 2 = - 12\]
So, the coordinates of C are (1, −12).
Also,
\[\left( \frac{x_2 + \left( - 1 \right)}{2}, \frac{y_2 + 0}{2} \right) = \left( 2, - 5 \right)\]
\[ \Rightarrow \frac{x_2 - 1}{2} = 2\ and\ \frac{y_2}{2} = - 5\]
\[ \Rightarrow x_2 - 1 = 4\ and\ y_2 = - 10\]
\[ \Rightarrow x_2 = 4 + 1 = 5\ and\ y_2 = - 10\]
APPEARS IN
संबंधित प्रश्न
Two vertices of a triangle are (3, –5) and (–7, 4). If its centroid is (2, –1). Find the third vertex
Prove that the diagonals of a rectangle bisect each other and are equal.
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
If the points A (6, 1), B (8, 2), C (9, 4) and D (k, p) are the vertices of a parallelogram taken in order, then find the values of k and p.
Find the co-ordinates of the points of tri-section of the line joining the points (–3, 0) and (6, 6).
The line joining P (-5, 6) and Q (3, 2) intersects the y-axis at R. PM and QN are perpendiculars from P and Q on the x-axis. Find the ratio PR: RQ.
Q is a point on the line segment AB. The coordinates of A and B are (2, 7) and (7, 12) along the line AB so that AQ = 4BQ. Find the coordinates of Q.
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P (- 3, 4) on AB divides it in the ratio 2 : 3. Find the coordinates of A and B.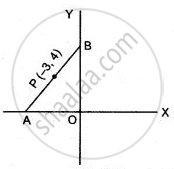
The point Q divides segment joining A(3, 5) and B(7, 9) in the ratio 2 : 3. Find the X-coordinate of Q
If A and B are (– 2, – 2) and (2, – 4) respectively; then find the co-ordinates of the point P such that `(AB)/(AB) = 3/7`.
