Question

If two adjacent vertices of a parallelogram are (3, 2) and (−1, 0) and the diagonals intersect at (2, −5), then find the coordinates of the other two vertices.

Answer 1

Let ABCD be the parallelogram with two adjacent vertices A(3, 2) and B(−1, 0). Suppose O(2, −5) be the point of intersection of the diagonals AC and BD.

Let C(x₁, y₁) and D(x₂, y₂) be the coordinates of the other vertices of the parallelogram.

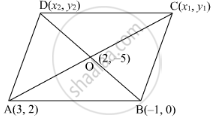
We know that the diagonals of the parallelogram bisect each other. Therefore, O is the mid-point of AC and BD.
Using the mid-point formula, we have

\[\left( \frac{x_1 + 3}{2}, \frac{y_1 + 2}{2} \right) = \left( 2, - 5 \right)\]

\[ \Rightarrow \frac{x_1 + 3}{2} = 2\ and\ \frac{y_1 + 2}{2} = - 5\]

\[ \Rightarrow x_1 + 3 = 4\ and\ y_1 + 2 = - 10\]

\[ \Rightarrow x_1 = 4 - 3 = 1\ and\ y_1 = - 10 - 2 = - 12\]

So, the coordinates of C are (1, −12).

Also,

\[\left( \frac{x_2 + \left( - 1 \right)}{2}, \frac{y_2 + 0}{2} \right) = \left( 2, - 5 \right)\]

\[ \Rightarrow \frac{x_2 - 1}{2} = 2\ and\ \frac{y_2}{2} = - 5\]

\[ \Rightarrow x_2 - 1 = 4\ and\ y_2 = - 10\]

\[ \Rightarrow x_2 = 4 + 1 = 5\ and\ y_2 = - 10\]

So, the coordinates of D are (5, −10).