Advertisements
Advertisements
Question
Find the coordinates of the point R on the line segment joining the points P(–1, 3) and Q(2, 5) such that PR = `3/5` PQ.
Solution
According to the question,

Given that,
PR = `3/5`PQ
⇒ `("PQ")/("PR") = 5/3`
⇒ `("PR" + "RQ")/("PR") = 5/3`
⇒ `1 + ("RQ")/("PR") = 5/3`
⇒ `("PQ")/("PR") = 5/3 - 1 = 2/3`
∴ RQ : PR = 2 : 3
or PR : RQ = 3 : 2
Suppose, R(x, y) be the point which divides the line segment joining the points P(–1, 3) and Q(2, 5) in the ratio 3 : 2
∴ (x, y) = `{(3(2) + 2(-1))/(3 + 2), (3(5) + 2(3))/(3 + 2)}` ...`[∵ "By internal section formula", {(m_2x_1 + m_1x_2)/(m_1 + m_2), (m_2y_1 + m_1y_2)/(m_1 + m_2)}]`
= `((6 - 2)/5, (15 + 6)/5)`
= `(4/5, 21/5)`
Hence, the required coordinates of the point R is `(4/5, 21/5)`.
APPEARS IN
RELATED QUESTIONS
Find the ratio in which y-axis divides the line segment joining the points A(5, –6) and B(–1, –4). Also find the coordinates of the point of division.
Find the coordinates of the point which divides the line segment joining the points (6, 3) and (– 4, 5) in the ratio 3 : 2 internally.
If the coordinates of the mid-points of the sides of a triangle are (1, 2) (0, –1) and (2, 1). Find the coordinates of its vertices.
P is a point on the line joining A(4, 3) and B(–2, 6) such that 5AP = 2BP. Find the co-ordinates of P.
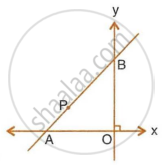
In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (−4, 2) and AP : PB = 1 : 2. Find the co-ordinates of A and B.
Find the co-ordinates of the centroid of a triangle ABC whose vertices are: A(–1, 3), B(1, –1) and C(5, 1).
Find the coordinate of a point P which divides the line segment joining :
5(2, 6) and R(9, -8) in the ratio 3: 4.
In what ratio does the point (1, a) divided the join of (−1, 4) and (4, −1) Also, find the value of a.
Find the coordinates of the points of trisection of the line segment joining the points (3, -3) and ( 6, 9).
If the points A(1, –2), B(2, 3) C(a, 2) and D(– 4, –3) form a parallelogram, find the value of a and height of the parallelogram taking AB as base.
