Advertisements
Advertisements
Question
Find the co-ordinates of the centroid of a triangle ABC whose vertices are: A(–1, 3), B(1, –1) and C(5, 1).
Solution
Co-ordinates of the centroid of triangle ABC are
`((-1 + 1 + 5)/(3),(3 - 1 + 1)/(3))`
= `(5/3, 1)`
APPEARS IN
RELATED QUESTIONS
Prove that (4, – 1), (6, 0), (7, 2) and (5, 1) are the vertices of a rhombus. Is it a square?
If the coordinates of the mid-points of the sides of a triangle are (1, 2) (0, –1) and (2, 1). Find the coordinates of its vertices.
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Find the coordinates of the points which divide the line segment joining A (−2, 2) and B (2, 8) into four equal parts.
A (–3, 4), B (3, –1) and C (–2, 4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies inside BC, such that BP : PC = 2 : 3.
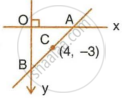
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
Find the lengths of the medians of a ΔABC whose vertices are A(0,-1) , B(2,1) and C (0.3).
M and N are two points on the X axis and Y axis respectively. P (3, 2) divides the line segment MN in the ratio 2 : 3.
Find:
(i) the coordinates of M and N
(ii) slope of the line MN.
The points A, B and C divides the line segment MN in four equal parts. The coordinates of Mand N are (-1, 10) and (7, -2) respectively. Find the coordinates of A, B and C.
If P(9a – 2, – b) divides line segment joining A(3a + 1, –3) and B(8a, 5) in the ratio 3 : 1, find the values of a and b.
