Advertisements
Advertisements
Question
M and N are two points on the X axis and Y axis respectively. P (3, 2) divides the line segment MN in the ratio 2 : 3.
Find:
(i) the coordinates of M and N
(ii) slope of the line MN.
Solution
Let coordinates of M is (a, 0) and M is (0, b).
Point P divides MN in 2 : 3 ratio
`therefore 3 =(3a + 2 xx 0 )/ (3 + 2) " and " 2 =(3xx0+2xx b)/(3+2)`
3a = 15 and 10 = 2b
a = 5 and b = 5
(i) The coordinates of M is (5, 0) and N(0, 5)
(ii) Slope of the line MN `= (0-5)/(5-0) = -1 `

APPEARS IN
RELATED QUESTIONS
Find the coordinates of points which trisect the line segment joining (1, –2) and (–3, 4)
Prove that the points (–2, –1), (1, 0), (4, 3) and (1, 2) are the vertices of a parallelogram. Is it a rectangle ?
If the points A (6, 1), B (8, 2), C (9, 4) and D (k, p) are the vertices of a parallelogram taken in order, then find the values of k and p.
In what ratio does the point (a, 6) divide the join of (–4, 3) and (2, 8)? Also, find the value of a.
Calculate the ratio in which the line joining the points (–3, –1) and (5, 7) is divided by the line x = 2. Also, find the co-ordinates of the point of intersection.
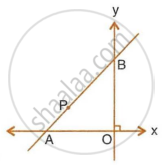
In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (−4, 2) and AP : PB = 1 : 2. Find the co-ordinates of A and B.
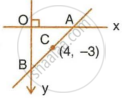
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
Find the coordinates of a point P, which lies on the line segment joining the points A (−2, −2), and B (2, −4), such that `AP=3/7 AB`.
If P(9a – 2, – b) divides line segment joining A(3a + 1, –3) and B(8a, 5) in the ratio 3 : 1, find the values of a and b.
Complete the following activity to find the coordinates of point P which divides seg AB in the ratio 3:1 where A(4, – 3) and B(8, 5).
Activity:
∴ By section formula,
∴ x = `("m"x_2 + "n"x_1)/square`,
∴ x = `(3 xx 8 + 1 xx 4)/(3 + 1)`,
= `(square + 4)/4`,
∴ x = `square`,
∴ y = `square/("m" + "n")`
∴ y = `(3 xx 5 + 1 xx (-3))/(3 + 1)`
= `(square - 3)/4`
∴ y = `square`
