Advertisements
Advertisements
प्रश्न
Find the ratio in which the line x = O divides the join of ( -4, 7) and (3, 0).
Also, find the coordinates of the point of intersection.
उत्तर

Let S (0, y) be the point on line x = 0 i.e. y-axis which divides the line segment PQ in the ratio k: 1.
Coordinates of S are,
`0 = (3"k" - 4)/("k + 1") ` Y = `(0 + 7)/("k" + 1)`
⇒ 3k = 4
k = `4/3` ..........(1)
Y = `7/(4/3 + 1)` ....(from (1))
Y = 3
Hence, the required ratio is 4 : 3 and the required point is S(O, 3).
APPEARS IN
संबंधित प्रश्न
If the point C (–1, 2) divides internally the line segment joining A (2, 5) and B in ratio 3 : 4, find the coordinates of B
Find the lengths of the medians of a triangle whose vertices are A (−1,3), B(1,−1) and C(5, 1).
Find the distance of the point (1, 2) from the mid-point of the line segment joining the points (6, 8) and (2, 4).
Show that the line segment joining the points (–5, 8) and (10, −4) is trisected by the co-ordinate axes.
The line segment joining the points M(5, 7) and N(–3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also, find the co-ordinates of L.
The line segment joining A (2, 3) and B (6, –5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the coordinates of the point K.
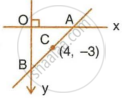
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
Find the coordinates of a point P, which lies on the line segment joining the points A (−2, −2), and B (2, −4), such that `AP=3/7 AB`.
Find the points of trisection of the segment joining A ( -3, 7) and B (3, -2).
The line segment joining the points A(3, 2) and B(5, 1) is divided at the point P in the ratio 1 : 2 and it lies on the line 3x – 18y + k = 0. Find the value of k.
