Advertisements
Advertisements
प्रश्न
Show that the line segment joining the points (–5, 8) and (10, −4) is trisected by the co-ordinate axes.
उत्तर
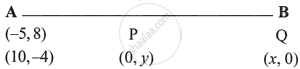
Let the points A (–5, 8) and B (10, −4).
Let P and Q be the two points on the axis which trisect the line joining the points A and B.
∵ AP = PQ = QB
∴ AP : PB = 1 : 2 and AQ : QB = 2 : 1
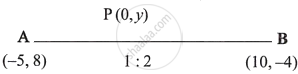
Now, co-ordinates of P will be,
`x = (1 xx 10 + 2 xx (-5))/(1 + 2)`
= `(10 - 10)/3`
= 0
y = `(1 xx (-4) + 2 xx 8)/(1 + 2)`
= `(-4 + 16)/3`
= `12/3`
= 4
∴ Co-ordinates of P are (0, 4)
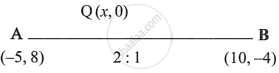
Co-ordinates of Q will be,
`x = (2 xx 10 + 1 xx (-5))/(2 + 1)`
= `(20 - 5)/3`
= `15/3`
= 5
`y = (2 xx (-4) + 1 xx 8)/(2 + 1)`
= `(-8 + 8)/3`
= `0/3`
= 0
∴ Co-ordinates of Q are (5, 0)
Hence Proved.
APPEARS IN
संबंधित प्रश्न
In what ratio does the x-axis divide the line segment joining the points (2, –3) and (5, 6)? Also, find the coordinates of the point of intersection.
If A(–2, –1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram, find the values of a and b
If the points (-2, -1), (1, 0), (x, 3) and (1, y) form a parallelogram, find the values of x and y.
If the points A (6, 1), B (8, 2), C (9, 4) and D (k, p) are the vertices of a parallelogram taken in order, then find the values of k and p.
The line segment joining A (2, 3) and B (6, –5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the coordinates of the point K.
If the point C (–1, 2) divides internally the line-segment joining the points A (2, 5) and B (x, y) in the ratio 3 : 4, find the value of x2 + y2 ?
A (2, 5), B (-1, 2) and C (5, 8) are the vertices of triangle ABC. Point P and Q lie on AB and AC respectively, such that AP: PB = AQ: QC = 1: 2. Calculate the coordinates of P and Q. Also, show that 3PQ = BC.
The perpendicular bisector of the line segment joining the points A(1, 5) and B(4, 6) cuts the y-axis at ______.
If the points A(1, –2), B(2, 3) C(a, 2) and D(– 4, –3) form a parallelogram, find the value of a and height of the parallelogram taking AB as base.
If (2, 4) is the mid-point of the line segment joining (6, 3) and (a, 5), then the value of a is ______.
