Advertisements
Advertisements
प्रश्न
If the points A(1, –2), B(2, 3) C(a, 2) and D(– 4, –3) form a parallelogram, find the value of a and height of the parallelogram taking AB as base.
उत्तर
In parallelogram, we know that, diagonals are bisects each other.
i.e., Mid-point of AC = Mid-point of BD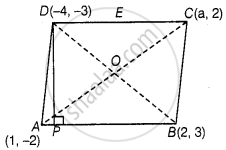
⇒ `((1 + a)/2, (-2 + 2)/2) = ((2 - 4)/2, (3 - 3)/2)` ...`["Since, mid-point of a line segment having points" (x_1, y_1) "and" (x_2, y_2) "is" ((x_1 + x_2)/2, (y_1 + y_2)/2)]`
⇒ `(1 + a)/2 = (2 - 4)/2 = (-2)/2` = – 1
⇒ 1 + a = – 2
⇒ a = – 3
So, the required value of a is – 3.
Given that, AB as base of a parallelogram and drawn a perpendicular from D to AB which meet AB at P.
So, DP is a height of a parallelogram.
Now, equation of base AB, passing through the points (1, – 2) and (2, 3) is
⇒ (y – y1) = `(y_2 - y_1)/(x_2 - x_1)(x - x_1)`
⇒ (y + 2) = `(3 + 2)/(2 - 1)(x - 1)`
⇒ (y + 2) = 5(x – 1)
⇒ 5x – y = 7 ...(i)
Slope of AB, say m1 = `(y_2 - y_1)/(x_2 - x_1) = (3 + 2)/(2 - 1)` = 5
Let the slope of DP be m2.
Since, DP is perpendicular to AB.
By condition of perpendicularity,
m1 · m2 = – 1
⇒ 5 · m2 = – 1
⇒ m2 = `-1/5`
Now, equation of DP, having slope `(-1/5)` and passing the point (– 4, – 3) is
(y – y1) = m2(x – x1)
⇒ (y + 3) = `-1/5(x + 4)`
⇒ 5y + 15 = – x – 4
⇒ x + 5y = – 19 ...(ii)
On adding equations (i) and (ii), then we get the intersection point P.
Put the value of y from equation (i) in equation (ii), we get
x + 5(5x – 7) = – 19 ...[Using equation (i)]
⇒ x + 25x – 35 = – 19
⇒ 26x = 16
∴ x = `8/13`
Put the value of x in equation (i), we get
y = `5(8/13) - 7 = 40/13 - 7`
⇒ y = `(40 - 91)/13`
⇒ y = `(-51)/13`
∴ Coordinates of point P ≡ `(8/13, (-51)/13)`
So, length of the height of a parallelogram,
DP = `sqrt((8/13 + 4)^2 + ((-51)/13 + 3)^2` ...`[∵ "By distance formula, distance between two points" (x_1, y_1) "and" (x_2, y_2) "is" d = sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)]`
⇒ DP = `sqrt((60/13)^2 + ((-12)/13)^2`
= `1/13 sqrt(3600 + 144)`
= `1/13 sqrt(3744)`
= `(12sqrt(26))/13`
Hence, the required length of height of a parallelogram is `(12sqrt(26))/13`.
APPEARS IN
संबंधित प्रश्न
Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
Determine the ratio in which the line 3x + y – 9 = 0 divides the segment joining the points (1, 3) and (2, 7)
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, –3). Hence find m.
Find the lengths of the medians of a ΔABC whose vertices are A(0,-1) , B(2,1) and C (0.3).
Find the coordinate of a point P which divides the line segment joining :
M( -4, -5) and N (3, 2) in the ratio 2 : 5.
Find the ratio in which the line x = -2 divides the line segment joining (-6, -1) and (1, 6). Find the coordinates of the point of intersection.
Find the ratio in which the point P (2, 4) divides the line joining points (-3, 1) and (7, 6).
Find the ratio in which Y-axis divides the point A(3, 5) and point B(– 6, 7). Find the coordinates of the point
In what ratio does the x-axis divide the line segment joining the points (– 4, – 6) and (–1, 7)? Find the coordinates of the point of division.
