Advertisements
Advertisements
प्रश्न
Find the ratio in which the line x = -2 divides the line segment joining (-6, -1) and (1, 6). Find the coordinates of the point of intersection.
उत्तर
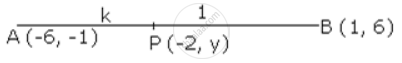
Let P (-2, y) be the pcint on line x which divides the line segment AB the ratio k : 1.
Coordinates of P are
`- 2 = ("k" - 6)/("k" + 1) ,`
⇒ -2k - 2 = k - 6
⇒ -3k = - 4
⇒ k = `4/3` .....(1)
`=> "k " = 4/3 `
y = `(6"k" - 1)/("k + 1")`
`=> "y" = (69 (4/3) - 1)/(4/3 + 1)` ...from (1)
`=> "y" = (24 - 3)/7 `
⇒ y = 3
Hence, the required ratio is 4: 3 and the point of intersection is (-2, 3).
APPEARS IN
संबंधित प्रश्न
The three vertices of a parallelogram taken in order are (–1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of the fourth vertex.
Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, –3). Hence find m.
The line segment joining A(4, 7) and B(−6, −2) is intercepted by the y – axis at the point K. write down the abscissa of the point K. hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K.
In what ratio is the line joining A(0, 3) and B(4, –1) divided by the x-axis? Write the co-ordinates of the point where AB intersects the x-axis.
The mid point of the line segment joining (4a, 2b – 3) and (−4, 3b) is (2, –2a). Find the values of a and b.
The three vertices of a parallelogram ABCD are A(3, −4), B(−1, −3) and C(−6, 2). Find the coordinates of vertex D and find the area of ABCD.
M and N are two points on the X axis and Y axis respectively. P (3, 2) divides the line segment MN in the ratio 2 : 3.
Find:
(i) the coordinates of M and N
(ii) slope of the line MN.
Find the coordinate of a point P which divides the line segment joining :
A(-8, -5) and B (7, 10) in the ratio 2:3.
Find the ratio in which the line x = O divides the join of ( -4, 7) and (3, 0).
Also, find the coordinates of the point of intersection.
Find the coordinates of point P which divides line segment joining A ( 3, -10) and B (3, 2) in such a way that PB: AB= 1.5.
