Advertisements
Advertisements
Question
Find the ratio in which the line x = -2 divides the line segment joining (-6, -1) and (1, 6). Find the coordinates of the point of intersection.
Solution
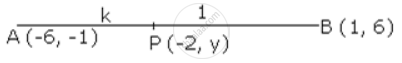
Let P (-2, y) be the pcint on line x which divides the line segment AB the ratio k : 1.
Coordinates of P are
`- 2 = ("k" - 6)/("k" + 1) ,`
⇒ -2k - 2 = k - 6
⇒ -3k = - 4
⇒ k = `4/3` .....(1)
`=> "k " = 4/3 `
y = `(6"k" - 1)/("k + 1")`
`=> "y" = (69 (4/3) - 1)/(4/3 + 1)` ...from (1)
`=> "y" = (24 - 3)/7 `
⇒ y = 3
Hence, the required ratio is 4: 3 and the point of intersection is (-2, 3).
APPEARS IN
RELATED QUESTIONS
Prove that the diagonals of a rectangle bisect each other and are equal.
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in the following figure. Niharika runs `1/4` th the distance AD on the 2nd line and posts a green flag. Preet runs `1/5` th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?

If two vertices of a parallelogram are (3, 2) (-1, 0) and the diagonals cut at (2, -5), find the other vertices of the parallelogram.
The line joining the points A (–3, –10) and B (–2, 6) is divided by the point P such that `(PB)/(AB) = 1/5`. Find the co-ordinates of P.
The line segment joining A(4, 7) and B(−6, −2) is intercepted by the y – axis at the point K. write down the abscissa of the point K. hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K.
Show that the line segment joining the points (-3, 10) and (6, -5) is trisected by the coordinates axis.
Find the ratio in which the line segment joining A (2, -3) and B(S, 6) i~ divided by the x-axis.
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, -5) is the mid-point of PQ, then the coordinates of P and Q are respectively.
The points (-5, 1), (1, p) and (4, -2) are collinear if the value of p is ______.
In what ratio does the Y-axis divide the line segment P(– 3, 1) and Q(6, 2)?
