Advertisements
Advertisements
प्रश्न
Find the ratio in which the line x = -2 divides the line segment joining (-6, -1) and (1, 6). Find the coordinates of the point of intersection.
उत्तर
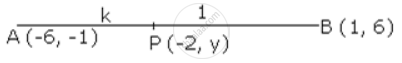
Let P (-2, y) be the pcint on line x which divides the line segment AB the ratio k : 1.
Coordinates of P are
`- 2 = ("k" - 6)/("k" + 1) ,`
⇒ -2k - 2 = k - 6
⇒ -3k = - 4
⇒ k = `4/3` .....(1)
`=> "k " = 4/3 `
y = `(6"k" - 1)/("k + 1")`
`=> "y" = (69 (4/3) - 1)/(4/3 + 1)` ...from (1)
`=> "y" = (24 - 3)/7 `
⇒ y = 3
Hence, the required ratio is 4: 3 and the point of intersection is (-2, 3).
APPEARS IN
संबंधित प्रश्न
Points A, B, C and D divide the line segment joining the point (5, –10) and the origin in five equal parts. Find the co-ordinates of B and D.
- Write down the co-ordinates of the point P that divides the line joining A(−4, 1) and B(17, 10) in the ratio 1 : 2.
- Calculate the distance OP, where O is the origin.
- In what ratio does the y-axis divide the line AB?
Find the coordinates of point P which divides line segment joining A ( 3, -10) and B (3, 2) in such a way that PB: AB= 1.5.
A (30, 20) and B ( 6, -4) are two fixed points. Find the coordinates of a point Pin AB such that 2PB = AP. Also, find the coordinates of some other point Qin AB such that AB = 6 AQ.
Find the ratio in which the point P (2, 4) divides the line joining points (-3, 1) and (7, 6).
Point P(– 4, 6) divides point A(– 6, 10) and B(m, n) in the ratio 2:1, then find the coordinates of point B
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, -5) is the mid-point of PQ, then the coordinates of P and Q are respectively.
If P(9a – 2, – b) divides line segment joining A(3a + 1, –3) and B(8a, 5) in the ratio 3 : 1, find the values of a and b.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of the point P on AD such that AP : PD = 2 : 1
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1
