Advertisements
Advertisements
Question
Find the ratio in which the line y = -1 divides the line segment joining (6, 5) and (-2, -11). Find the coordinates of the point of intersection.
Solution
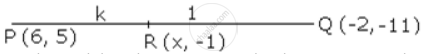
Let R (x, -1) be the point on the line y = - 1 which divides the line segment PQ in the ratio k: 1.
Coordinates of R are,
x = `(2"k" + 6)/("k" + 1) ,` -1 = `(-11 "k" + 5)/("k" + 1)`
x = `(-2 (3/5) + 6)/(3/5 + 1), => - "k" - 1 = - 11 "k" + 5`
`=> "x" = (-6 + 30)/8 => 10 "k" = 6`
x = 3 ⇒ k = 3/5 .....(1)
Hence, the required ratio is 3: 5 and the point of inter sec tion is (3, - 1).
APPEARS IN
RELATED QUESTIONS
The three vertices of a parallelogram taken in order are (–1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of the fourth vertex.
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in the following figure. Niharika runs `1/4` th the distance AD on the 2nd line and posts a green flag. Preet runs `1/5` th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?

If A and B are (−2, −2) and (2, −4), respectively, find the coordinates of P such that `"AP" = 3/7 "AB"` and P lies on the line segment AB.
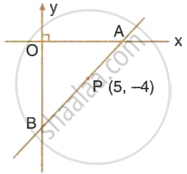
The point P (5, – 4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B. Given AP is smaller than BP.
The line segment joining A (2, 3) and B (6, –5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the coordinates of the point K.
In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (−4, 2) and AP : PB = 1 : 2. Find the co-ordinates of A and B.
If the point C (–1, 2) divides internally the line-segment joining the points A (2, 5) and B (x, y) in the ratio 3 : 4, find the value of x2 + y2 ?
Show that the line segment joining the points (-3, 10) and (6, -5) is trisected by the coordinates axis.
If A and B are (– 2, – 2) and (2, – 4) respectively; then find the co-ordinates of the point P such that `(AB)/(AB) = 3/7`.
What is the ratio in which the line segment joining (2, -3) and (5, 6) is divided by x-axis?
