Question

Students of a school are standing in rows and columns in their playground for a drill practice. A, B, C and D are the positions of four students as shown in figure. Is it possible to place Jaspal in the drill in such a way that he is equidistant from each of the four students A, B, C and D? If so, what should be his position?

Answer 1

Yes, from the figure we observe that the positions of four students A, B, C and D are (3, 5), (7, 9), (11, 5) and (7, 1) respectively i.e., these are four vertices of a quadrilateral.

Now, we will find the type of this quadrilateral.

For this, we will find all its sides.

We see that, AB = BC = CD = DA i.e., all sides are equal.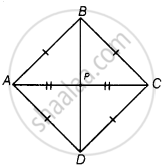

Now, AB = `sqrt((7 - 3)^2 + (9 - 5)^2`   ...`["By distance formula", d = sqrt((x_2  - x_1)^2 + (y_2 - y_1)^2)]`

AB = `sqrt((4)^2 + (4)^2`

= `sqrt(16 + 16)`

AB = `4sqrt(2)`

BC = `sqrt((11 - 7)^2 + (5 - 9)^2`

= `sqrt((4)^2 + (-4)^2`

= `sqrt(16 + 16)`

= `4sqrt(2)`

CD = `sqrt((7 - 11)^2 + (1 - 5)^2`

= `sqrt((-4)^2 + (-4)^2`

= `sqrt(16 + 16)`

= `4sqrt(2)`

And DA = `sqrt((3 - 7)^2 + (5 - 1)^2`

= `sqrt((-4)^2 + (4)^2`

= `sqrt(16 + 16)`

= `4sqrt(2)`

We see that, AB = BC = CD = DA i.e., all sides are equal.

Now, we find length of both diagonals.

AC = `sqrt((11 - 3)^2 + (5 - 5)^2`

= `sqrt((8)^2 + 0)`

= 8

And BD = `sqrt((7 - 7)^2 + (1 - 9)^2`

= `sqrt(0 + (-8)^2`

= 8

Here, AC = BD

Since, AB = BC = CD = DA and AC = BD

Which represent a square.

Also known the diagonals of a square bisect each other.

So, P be position of Jaspal in which he is equidistant from each of the four students A, B, C and D.

∴ Coordinates of point P = Mid-point of AC

= `((3 + 11)/2, (5 + 5)/2)`  ...`[∵ "Since, mid-point of a line segment having points"  (x_1, y_1)  "and"  (x_2, y_2) = ((x_1 + y_1)/2, (x_2 + y_2)/2)]`

= `(14/2, 10/2)`

= (7, 5)

Hence, the required position of Jaspal is (7, 5).