Advertisements
Advertisements
प्रश्न
Students of a school are standing in rows and columns in their playground for a drill practice. A, B, C and D are the positions of four students as shown in figure. Is it possible to place Jaspal in the drill in such a way that he is equidistant from each of the four students A, B, C and D? If so, what should be his position?
उत्तर
Yes, from the figure we observe that the positions of four students A, B, C and D are (3, 5), (7, 9), (11, 5) and (7, 1) respectively i.e., these are four vertices of a quadrilateral.
Now, we will find the type of this quadrilateral.
For this, we will find all its sides.
We see that, AB = BC = CD = DA i.e., all sides are equal.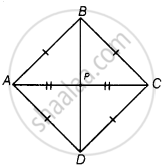
Now, AB = `sqrt((7 - 3)^2 + (9 - 5)^2` ...`["By distance formula", d = sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)]`
AB = `sqrt((4)^2 + (4)^2`
= `sqrt(16 + 16)`
AB = `4sqrt(2)`
BC = `sqrt((11 - 7)^2 + (5 - 9)^2`
= `sqrt((4)^2 + (-4)^2`
= `sqrt(16 + 16)`
= `4sqrt(2)`
CD = `sqrt((7 - 11)^2 + (1 - 5)^2`
= `sqrt((-4)^2 + (-4)^2`
= `sqrt(16 + 16)`
= `4sqrt(2)`
And DA = `sqrt((3 - 7)^2 + (5 - 1)^2`
= `sqrt((-4)^2 + (4)^2`
= `sqrt(16 + 16)`
= `4sqrt(2)`
We see that, AB = BC = CD = DA i.e., all sides are equal.
Now, we find length of both diagonals.
AC = `sqrt((11 - 3)^2 + (5 - 5)^2`
= `sqrt((8)^2 + 0)`
= 8
And BD = `sqrt((7 - 7)^2 + (1 - 9)^2`
= `sqrt(0 + (-8)^2`
= 8
Here, AC = BD
Since, AB = BC = CD = DA and AC = BD
Which represent a square.
Also known the diagonals of a square bisect each other.
So, P be position of Jaspal in which he is equidistant from each of the four students A, B, C and D.
∴ Coordinates of point P = Mid-point of AC
= `((3 + 11)/2, (5 + 5)/2)` ...`[∵ "Since, mid-point of a line segment having points" (x_1, y_1) "and" (x_2, y_2) = ((x_1 + y_1)/2, (x_2 + y_2)/2)]`
= `(14/2, 10/2)`
= (7, 5)
Hence, the required position of Jaspal is (7, 5).
APPEARS IN
संबंधित प्रश्न
A (3, 2) and B (−2, 1) are two vertices of a triangle ABC whose centroid G has the coordinates `(5/3,-1/3)`Find the coordinates of the third vertex C of the triangle.
Find the point on x-axis which is equidistant from the points (−2, 5) and (2,−3).
Find the ratio in which the line segment joining (-2, -3) and (5, 6) is divided by x-axis Also, find the coordinates of the point of division in each case.
Prove that the points (4, 5) (7, 6), (6, 3) (3, 2) are the vertices of a parallelogram. Is it a rectangle.
Prove that (4, 3), (6, 4) (5, 6) and (3, 5) are the angular points of a square.
Determine the ratio in which the point P (m, 6) divides the join of A(-4, 3) and B(2, 8). Also, find the value of m.
Show hat A(1,2), B(4,3),C(6,6) and D(3,5) are the vertices of a parallelogram. Show that ABCD is not rectangle.
Find the area of quadrilateral ABCD whose vertices are A(-3, -1), B(-2,-4) C(4,-1) and D(3,4)
Show that A(-4, -7), B(-1, 2), C(8, 5) and D(5, -4) are the vertices of a
rhombus ABCD.
The abscissa of any point on y-axis is
Show that the points (−4, −1), (−2, −4) (4, 0) and (2, 3) are the vertices points of a rectangle.
If A(3, y) is equidistant from points P(8, −3) and Q(7, 6), find the value of y and find the distance AQ.
If three points (x1, y1) (x2, y2), (x3, y3) lie on the same line, prove that \[\frac{y_2 - y_3}{x_2 x_3} + \frac{y_3 - y_1}{x_3 x_1} + \frac{y_1 - y_2}{x_1 x_2} = 0\]
If the points A(−2, 1), B(a, b) and C(4, −1) ae collinear and a − b = 1, find the values of aand b.
Write the distance between the points A (10 cos θ, 0) and B (0, 10 sin θ).
If the points A (1,2) , O (0,0) and C (a,b) are collinear , then find a : b.
If P is a point on x-axis such that its distance from the origin is 3 units, then the coordinates of a point Q on OY such that OP = OQ, are
If the points P (x, y) is equidistant from A (5, 1) and B (−1, 5), then
If segment AB is parallel Y-axis and coordinates of A are (1, 3), then the coordinates of B are ______
Point (3, 0) lies in the first quadrant.
