Advertisements
Advertisements
प्रश्न
Find the point on x-axis which is equidistant from the points (−2, 5) and (2,−3).
उत्तर
The distance d between two points `(x_1, y_1)` and `(x_2,y_2)` is given by the formula
Here we are to find out a point on the x-axis which is equidistant from both the points A(−2,5) and B(2,−3)
Let this point be denoted as C(x, y).
Since the point lies on the x-axis the value of its ordinate will be 0. Or in other words, we have y = 0.
Now let us find out the distances from ‘A’ and ‘B’ to ‘C’
`AC = sqrt((-2-x)^2 + (5 - y)^2)`
`= sqrt((-2 - x)^2 + (5 - 0))`
`AC = sqrt((-2-x)^2 + (5)^2)`
`BC = sqrt((2 - x)^2 + (-3-0)^2)`
`= sqrt((2 - x)^2 + (-3-0)^2)`
`BC = sqrt((2 - x)^2 + (-3)^2)`
We know that both these distances are the same. So equating both these we get,
AC = BC
`sqrt((-2-x)^2 + (5)^2) = sqrt((2 - x)^2 + (-3)^2)`
Squaring on both sides we have,
`(-2-x)^2 + (5)^2 = (2 - x)^2 + (-3)^2`
`4 + x^2 + 4x + 25 = 4 + x^2 - 4x + 9`
8x = -16
x = -2
Hence the point on the x-axis which lies at equal distances from the mentioned points is (-2, 0)
APPEARS IN
संबंधित प्रश्न
On which axis do the following points lie?
P(5, 0)
Find the equation of the perpendicular bisector of the line segment joining points (7, 1) and (3,5).
In what ratio is the line segment joining (-3, -1) and (-8, -9) divided at the point (-5, -21/5)?
Determine the ratio in which the straight line x - y - 2 = 0 divides the line segment
joining (3, -1) and (8, 9).
Show that the points A(3,0), B(4,5), C(-1,4) and D(-2,-1) are the vertices of a rhombus. Find its area.
If the points P (a,-11) , Q (5,b) ,R (2,15) and S (1,1). are the vertices of a parallelogram PQRS, find the values of a and b.
Find the ratio in which the point (−3, k) divides the line-segment joining the points (−5, −4) and (−2, 3). Also find the value of k ?
Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles.
ABCD is a parallelogram with vertices \[A ( x_1 , y_1 ), B \left( x_2 , y_2 \right), C ( x_3 , y_3 )\] . Find the coordinates of the fourth vertex D in terms of \[x_1 , x_2 , x_3 , y_1 , y_2 \text{ and } y_3\]
If A(−3, 5), B(−2, −7), C(1, −8) and D(6, 3) are the vertices of a quadrilateral ABCD, find its area.
Write the perimeter of the triangle formed by the points O (0, 0), A (a, 0) and B (0, b).
Write the coordinates the reflections of points (3, 5) in X and Y -axes.
If the centroid of a triangle is (1, 4) and two of its vertices are (4, −3) and (−9, 7), then the area of the triangle is
If (−2, 1) is the centroid of the triangle having its vertices at (x , 0) (5, −2), (−8, y), then x, y satisfy the relation
If A(4, 9), B(2, 3) and C(6, 5) are the vertices of ∆ABC, then the length of median through C is
Find the point on the y-axis which is equidistant from the points (S, - 2) and (- 3, 2).
Abscissa of all the points on the x-axis is ______.
Seg AB is parallel to X-axis and coordinates of the point A are (1, 3), then the coordinates of the point B can be ______.
In which ratio the y-axis divides the line segment joining the points (5, – 6) and (–1, – 4)?
Ryan, from a very young age, was fascinated by the twinkling of stars and the vastness of space. He always dreamt of becoming an astronaut one day. So, he started to sketch his own rocket designs on the graph sheet. One such design is given below :
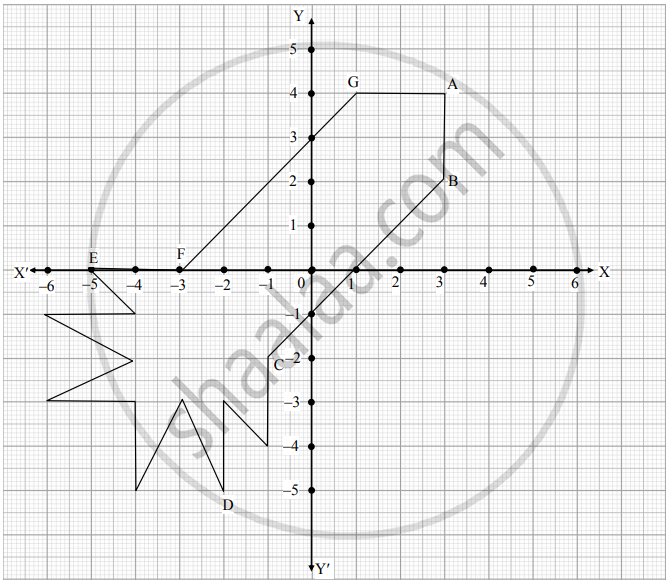
Based on the above, answer the following questions:
i. Find the mid-point of the segment joining F and G. (1)
ii. a. What is the distance between the points A and C? (2)
OR
b. Find the coordinates of the points which divides the line segment joining the points A and B in the ratio 1 : 3 internally. (2)
iii. What are the coordinates of the point D? (1)
