Advertisements
Advertisements
प्रश्न
If the points P (a,-11) , Q (5,b) ,R (2,15) and S (1,1). are the vertices of a parallelogram PQRS, find the values of a and b.
उत्तर
The points are P (a,-11),Q(5,b) , R (2,15) and S(1,1).
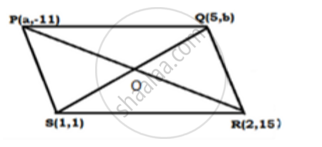
Join PR and QS, intersecting at O.
We know that the diagonals of a parallelogram bisect each other Therefore, O is the midpoint of PR as well as QS.
`"Midpoint of PR" = ((a+2)/2,(-11+15)/2) = ((a+2)/2,4/2) = ((a+2)/2,2)`
`"Midpoint of QS " = ((5+1)/2 , (b+1)/2) = (6/2 ,(b+1)/2) = (3,(b+1)/2)`
Therefore , `(a+2)/2 =3, (b+1)/2= 2`
⇒ a +2 = 6, b+1=4
⇒ a = 6 - 2, b = 4-1
⇒ a = 4 and b= 3
APPEARS IN
संबंधित प्रश्न
If the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k − 1, 5k) are collinear, then find the value of k
Find the distance between the following pair of points:
(a, 0) and (0, b)
Prove that the points (3, 0), (4, 5), (-1, 4) and (-2, -1), taken in order, form a rhombus.
Also, find its area.
Find the coordinates of the point where the diagonals of the parallelogram formed by joining the points (-2, -1), (1, 0), (4, 3) and(1, 2) meet
Show that the points A(6,1), B(8,2), C(9,4) and D(7,3) are the vertices of a rhombus. Find its area.
Show that the following points are the vertices of a rectangle.
A (2, -2), B(14,10), C(11,13) and D(-1,1)
In what ratio does the point P(2,5) divide the join of A (8,2) and B(-6, 9)?
ΔXYZ ∼ ΔPYR; In ΔXYZ, ∠Y = 60o, XY = 4.5 cm, YZ = 5.1 cm and XYPY =` 4/7` Construct ΔXYZ and ΔPYR.
Mark the correct alternative in each of the following:
The point of intersect of the coordinate axes is
Find the value of a for which the area of the triangle formed by the points A(a, 2a), B(−2, 6) and C(3, 1) is 10 square units.
Find the value(s) of k for which the points (3k − 1, k − 2), (k, k − 7) and (k − 1, −k − 2) are collinear.
what is the value of \[\frac{a^2}{bc} + \frac{b^2}{ca} + \frac{c^2}{ab}\] .
Write the condition of collinearity of points (x1, y1), (x2, y2) and (x3, y3).
If (x , 2), (−3, −4) and (7, −5) are collinear, then x =
If the centroid of the triangle formed by (7, x) (y, −6) and (9, 10) is at (6, 3), then (x, y) =
If the points(x, 4) lies on a circle whose centre is at the origin and radius is 5, then x =
Find the point on the y-axis which is equidistant from the points (S, - 2) and (- 3, 2).
What are the coordinates of origin?
The distance of the point P(2, 3) from the x-axis is ______.
Points (1, –1) and (–1, 1) lie in the same quadrant.
