Advertisements
Advertisements
प्रश्न
If the points A(1, –2), B(2, 3) C(a, 2) and D(– 4, –3) form a parallelogram, find the value of a and height of the parallelogram taking AB as base.
उत्तर
In parallelogram, we know that, diagonals are bisects each other.
i.e., Mid-point of AC = Mid-point of BD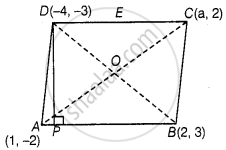
⇒ `((1 + a)/2, (-2 + 2)/2) = ((2 - 4)/2, (3 - 3)/2)` ...`["Since, mid-point of a line segment having points" (x_1, y_1) "and" (x_2, y_2) "is" ((x_1 + x_2)/2, (y_1 + y_2)/2)]`
⇒ `(1 + a)/2 = (2 - 4)/2 = (-2)/2` = – 1
⇒ 1 + a = – 2
⇒ a = – 3
So, the required value of a is – 3.
Given that, AB as base of a parallelogram and drawn a perpendicular from D to AB which meet AB at P.
So, DP is a height of a parallelogram.
Now, equation of base AB, passing through the points (1, – 2) and (2, 3) is
⇒ (y – y1) = `(y_2 - y_1)/(x_2 - x_1)(x - x_1)`
⇒ (y + 2) = `(3 + 2)/(2 - 1)(x - 1)`
⇒ (y + 2) = 5(x – 1)
⇒ 5x – y = 7 ...(i)
Slope of AB, say m1 = `(y_2 - y_1)/(x_2 - x_1) = (3 + 2)/(2 - 1)` = 5
Let the slope of DP be m2.
Since, DP is perpendicular to AB.
By condition of perpendicularity,
m1 · m2 = – 1
⇒ 5 · m2 = – 1
⇒ m2 = `-1/5`
Now, equation of DP, having slope `(-1/5)` and passing the point (– 4, – 3) is
(y – y1) = m2(x – x1)
⇒ (y + 3) = `-1/5(x + 4)`
⇒ 5y + 15 = – x – 4
⇒ x + 5y = – 19 ...(ii)
On adding equations (i) and (ii), then we get the intersection point P.
Put the value of y from equation (i) in equation (ii), we get
x + 5(5x – 7) = – 19 ...[Using equation (i)]
⇒ x + 25x – 35 = – 19
⇒ 26x = 16
∴ x = `8/13`
Put the value of x in equation (i), we get
y = `5(8/13) - 7 = 40/13 - 7`
⇒ y = `(40 - 91)/13`
⇒ y = `(-51)/13`
∴ Coordinates of point P ≡ `(8/13, (-51)/13)`
So, length of the height of a parallelogram,
DP = `sqrt((8/13 + 4)^2 + ((-51)/13 + 3)^2` ...`[∵ "By distance formula, distance between two points" (x_1, y_1) "and" (x_2, y_2) "is" d = sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)]`
⇒ DP = `sqrt((60/13)^2 + ((-12)/13)^2`
= `1/13 sqrt(3600 + 144)`
= `1/13 sqrt(3744)`
= `(12sqrt(26))/13`
Hence, the required length of height of a parallelogram is `(12sqrt(26))/13`.
APPEARS IN
संबंधित प्रश्न
If the point C (–1, 2) divides internally the line segment joining A (2, 5) and B in ratio 3 : 4, find the coordinates of B
In what ratio does the point `(24/11, y)` divide the line segment joining the points P(2, –2) and Q(3, 7)? Also find the value of y.
P is a point on the line joining A(4, 3) and B(–2, 6) such that 5AP = 2BP. Find the co-ordinates of P.
A line segment joining A`(-1,5/3)` and B(a, 5) is divided in the ratio 1 : 3 at P, the point where the line segment AB intersects the y-axis.
- Calculate the value of ‘a’.
- Calculate the co-ordinates of ‘P’.
The mid point of the line segment joining (4a, 2b – 3) and (−4, 3b) is (2, –2a). Find the values of a and b.
Find the ratio in which the point P (2, 4) divides the line joining points (-3, 1) and (7, 6).
Find the ratio in which the point R ( 1, 5) divides the line segment joining the points S (-2, -1) and T (5, 13).
The vertices of a parallelogram in order are A(1, 2), B(4, y), C(x, 6) and D(3, 5). Then (x, y) is ______.
Point C divides the line segment whose points are A(4, –6) and B(5, 9) in the ratio 2:1. Find the coordinates of C.
Find the co-ordinates of the points of trisection of the line segment joining the points (5, 3) and (4, 5).
