Advertisements
Advertisements
प्रश्न
The mid point of the line segment joining (4a, 2b – 3) and (−4, 3b) is (2, –2a). Find the values of a and b.
उत्तर
It is given that the mid-point of the line segment joining (4a, 2b – 3) and (−4, 3b) is (2, –2a).
∴ `(2, -2a) = ((4a - 4)/2,(2b - 3 + 3b)/2)`
`=> 2 = ((4a - 4)/2)`
`=>` 4a − 4 = 4
`=>` 4a = 8
`=>` a = 2
Also,
`-2a = (2b - 3 + 3b)/2`
`=> -2 xx 2 = (5b - 3)/2`
`=>` 5b − 3 = −8
`=>` 5b = −5
`=>` b = −1
APPEARS IN
संबंधित प्रश्न
Find the coordinates of points which trisect the line segment joining (1, –2) and (–3, 4)
If A(–2, –1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram, find the values of a and b
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
The line segment joining the points (3, -4) and (1, 2) is trisected at the points P and Q. If the coordinates of P and Q are (p, -2) and (5/3, q) respectively. Find the values of p and q.
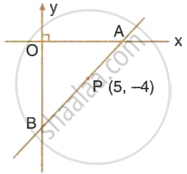
The point P (5, – 4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B. Given AP is smaller than BP.
A(20, 0) and B(10, –20) are two fixed points. Find the co-ordinates of the point P in AB such that : 3PB = AB. Also, find the co-ordinates of some other point Q in AB such that : AB = 6 AQ.
Find the ratio in which the line x = O divides the join of ( -4, 7) and (3, 0).
Also, find the coordinates of the point of intersection.
Find the ratio in which the line 2x + 3y – 5 = 0 divides the line segment joining the points (8, –9) and (2, 1). Also find the coordinates of the point of division.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of the point P on AD such that AP : PD = 2 : 1
Point C divides the line segment whose points are A(4, –6) and B(5, 9) in the ratio 2:1. Find the coordinates of C.
