Advertisements
Advertisements
प्रश्न
Find the co-ordinates of the points of trisection of the line segment joining the points (5, 3) and (4, 5).
उत्तर
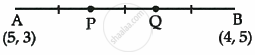
Given: AP = PQ = BQ
∴ `(AP)/(BP) = 1/2`
and `(AQ)/(BQ) = 2/1`
Coordinate of P = `(m_1x_2 + m_2x_1)/(m_1 + m_2), (m_1y_2 + m_2y_1)/(m_1 + m_2)`
= `(1 xx 4 + 2 xx 5)/(1 + 2), (1 xx 5 + 2 xx 3)/(1 + 2)`
= `(14/3, 11/3)`
Coordinate of Q = `(2 xx 4 + 1 xx 5)/(1 + 2), (2 xx 5 + 1 xx 3)/(1 + 2)`
= `(13/3, 13/3)`
APPEARS IN
संबंधित प्रश्न
Find the ratio in which the point P(x, 2) divides the line segment joining the points A(12, 5) and B(4, −3). Also, find the value of x.
Prove that the points (–2, –1), (1, 0), (4, 3) and (1, 2) are the vertices of a parallelogram. Is it a rectangle ?
If the mid-point of the line joining (3, 4) and (k, 7) is (x, y) and 2x + 2y + 1 = 0 find the value of k.
Find the ratio in which the join of (–4, 7) and (3, 0) is divided by the y-axis. Also, find the co-ordinates of the point of intersection.
Calculate the ratio in which the line joining A(6, 5) and B(4, –3) is divided by the line y = 2.
Using section formula, show that the points A(7, −5), B(9, −3) and C(13, 1) are collinear
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. The median from A meets BC at D. Find the coordinates of the point D.
The fourth vertex D of a parallelogram ABCD, whose three vertices are A(–2, 3), B(6, 7) and C(8, 3), is ______.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of the point P on AD such that AP : PD = 2 : 1
What is the ratio in which the line segment joining (2, -3) and (5, 6) is divided by x-axis?
