Question

The fourth vertex D of a parallelogram ABCD, whose three vertices are A(–2, 3), B(6, 7) and C(8, 3), is ______.

विकल्प

• (0, 1)

• (0, –1)

• (–1, 0)

• (1, 0)

Answer 1

The fourth vertex D of a parallelogram ABCD, whose three vertices are A(–2, 3), B(6, 7), and C(8, 3) is (0, –1).

Explanation:

Let the fourth vertex of the parallelogram, D ≡ (x_4, y₄) and L, M be the middle points of AC and BD, respectively,

Then, `L ≡ ((-2 + 8)/2, (3 + 3)/2) ≡ (3, 3)` and `M ≡ ((6 + x_4)/2, (7 + y_4)/2)`  ...`["Since mid-point of a line segment having points"  (x_1, y_1)  "and"  (x_2, y_2) = ((x_1 + x_2)/2, (y_1 + y_2)/2)]`

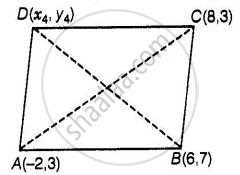
Since, ABCD is a parallelogram, therefore diagonals AC and BD will bisect each other.

Hence, L and M are the same points.

∴ 3 = `(6 + x_4)/2` and 3 = `(7 + y_4)/2`

⇒ 6 = 6 + x₄ and 6 = 7 + y₄

⇒ x₄ = 0 and y₄ = 6 – 7

∴ x₄ = 0 and y₄ = –1

Hence, the fourth vertex of the parallelogram is D = (x₄, y₄) = (0, –1).