Advertisements
Advertisements
प्रश्न
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. What are the coordinates of the centroid of the triangle ABC?
उत्तर
According to the question,
The vertices of ΔABC = A, B and C
Coordinates of A, B and C = A(x1, y1), B(x2, y2), C(x3, y3)
Coordinate of the centroid of the ΔABC;
= `("Sum of all coordinates of all vertices"/3, "Sum of all coordinates of all vertices"/3)`
= `((x_1 + x_2 + x_3)/3, (y_1 + y_2 + y_3)/3)`
APPEARS IN
संबंधित प्रश्न
Find the coordinates of a point P on the line segment joining A(1, 2) and B(6, 7) such that AP =(2/5)AB.
Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
Find the lengths of the medians of a ∆ABC whose vertices are A(7, –3), B(5,3) and C(3,–1)
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (− 1, 4) and (− 2, −1) taken in order.
[Hint: Area of a rhombus = `1/2` (product of its diagonals)]
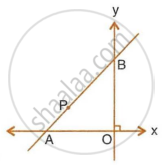
In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (−4, 2) and AP : PB = 1 : 2. Find the co-ordinates of A and B.
The point Q divides segment joining A(3, 5) and B(7, 9) in the ratio 2 : 3. Find the X-coordinate of Q
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, -5) is the mid-point of PQ, then the coordinates of P and Q are respectively.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1
In what ratio does the Y-axis divide the line segment P(– 3, 1) and Q(6, 2)?
Read the following passage:
Jagdish has a field which is in the shape of a right angled triangle AQC. He wants to leave a space in the form of a square PQRS inside the field for growing wheat and the remaining for growing vegetables (as shown in the figure). In the field, there is a pole marked as O. |
Based on the above information, answer the following questions :
- Taking O as origin, coordinates of P are (–200, 0) and of Q are (200, 0). PQRS being a square, what are the coordinates of R and S?
- (a) What is the area of square PQRS?
OR
(b) What is the length of diagonal PR in square PQRS? - If S divides CA in the ratio K : 1, what is the value of K, where point A is (200, 800)?
