Advertisements
Advertisements
प्रश्न
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (− 1, 4) and (− 2, −1) taken in order.
[Hint: Area of a rhombus = `1/2` (product of its diagonals)]
उत्तर

Let (3, 0), (4, 5), (−1, 4) and (−2, −1) are the vertices A, B, C, D of a rhombus ABCD.
Length of diagonal AC = `sqrt([3-(-1)]^2 + (0-4)^2)`
= `sqrt((-4)^2 + (4)^2)`
= `sqrt (16 + 16)`
= `4sqrt2`
Length of diagonal BD = `sqrt([4-(-2)]^2+[5-(-1)]^2)`
= `sqrt((-6)^2 + (-6)^2)`
= `sqrt(36+36) `
= `6sqrt2`
Therefore, area of rhombus ABCD = `1/2xx("Product of diagonals")`
= `1/2xx"AC"xx"BD"`
= `1/2xx4sqrt2xx6sqrt2`
= `1/2xx2xx4xx6`
= 24 square units
APPEARS IN
संबंधित प्रश्न
If A(–2, –1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram, find the values of a and b
Find the coordinates of the centroid of a triangle whose vertices are (–1, 0), (5, –2) and (8, 2)
If a vertex of a triangle be (1, 1) and the middle points of the sides through it be (-2,-3) and (5 2) find the other vertices.
Three vertices of a parallelogram are (a+b, a-b), (2a+b, 2a-b), (a-b, a+b). Find the fourth vertex.
Show that the line segment joining the points (–5, 8) and (10, −4) is trisected by the co-ordinate axes.
The line segment joining the points M(5, 7) and N(–3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also, find the co-ordinates of L.
A (2, 5), B (–1, 2) and C (5, 8) are the co-ordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that : AP : PB = AQ : QC = 1 : 2.
- Calculate the co-ordinates of P and Q.
- Show that : `PQ = 1/3 BC`.
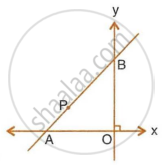
In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (−4, 2) and AP : PB = 1 : 2. Find the co-ordinates of A and B.
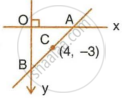
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
If two adjacent vertices of a parallelogram are (3, 2) and (−1, 0) and the diagonals intersect at (2, −5), then find the coordinates of the other two vertices.
Find the coordinates of a point P, which lies on the line segment joining the points A (−2, −2), and B (2, −4), such that `AP=3/7 AB`.
Find the coordinate of a point P which divides the line segment joining :
D(-7, 9) and E( 15, -2) in the ratio 4:7.
Find the ratio in which the line x = O divides the join of ( -4, 7) and (3, 0).
Also, find the coordinates of the point of intersection.
A (2, 5), B (-1, 2) and C (5, 8) are the vertices of triangle ABC. Point P and Q lie on AB and AC respectively, such that AP: PB = AQ: QC = 1: 2. Calculate the coordinates of P and Q. Also, show that 3PQ = BC.
In what ratio is the line joining (2, -1) and (-5, 6) divided by the y axis ?
The fourth vertex D of a parallelogram ABCD, whose three vertices are A(–2, 3), B(6, 7) and C(8, 3), is ______.
Find the ratio in which the point `P(3/4, 5/12)` divides the line segment joining the points `A(1/2, 3/2)` and B(2, –5).
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1
Complete the following activity to find the coordinates of point P which divides seg AB in the ratio 3:1 where A(4, – 3) and B(8, 5).
Activity:
∴ By section formula,
∴ x = `("m"x_2 + "n"x_1)/square`,
∴ x = `(3 xx 8 + 1 xx 4)/(3 + 1)`,
= `(square + 4)/4`,
∴ x = `square`,
∴ y = `square/("m" + "n")`
∴ y = `(3 xx 5 + 1 xx (-3))/(3 + 1)`
= `(square - 3)/4`
∴ y = `square`
