Advertisements
Advertisements
प्रश्न
In what ratio does the Y-axis divide the line segment P(– 3, 1) and Q(6, 2)?
उत्तर
Let the line segment PQ be divided by the Y-axis in the ratio k : 1.
Let A be the intersection's point (x, y).
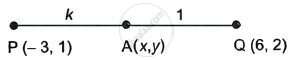
Then, using the section formula,
x = `(mx_2 + nx_1)/(m + n)`
⇒ x = `(6 xx k + (-3) xx 1)/(k + 1)`
⇒ x = `(6k - 3)/(k + 1)`
Now, on Y-axis, x-coordinate = 0
∴ `(6k - 3)/(k + 1)` = 0
⇒ 6k – 3 = 0
⇒ 6k = 3
⇒ k = `3/6 = 1/2`
∴ Ratio = `1/2` : 1 = 1 : 2
As a result, the needed ratio is 1 : 2.
APPEARS IN
संबंधित प्रश्न
Find the ratio in which y-axis divides the line segment joining the points A(5, –6) and B(–1, –4). Also find the coordinates of the point of division.
Find the coordinates of points which trisect the line segment joining (1, –2) and (–3, 4)
If the point C (–1, 2) divides internally the line segment joining A (2, 5) and B in ratio 3 : 4, find the coordinates of B
Prove that the points (–2, –1), (1, 0), (4, 3) and (1, 2) are the vertices of a parallelogram. Is it a rectangle ?
If the points A (6, 1), B (8, 2), C(9, 4) and D(p, 3) are vertices of a parallelogram, taken in order, find the value of p
If the coordinates of the mid-points of the sides of a triangle are (1, 2) (0, –1) and (2, 1). Find the coordinates of its vertices.
Find the lengths of the medians of a ∆ABC whose vertices are A(7, –3), B(5,3) and C(3,–1)
Find the coordinates of a point A, where AB is the diameter of circle whose centre is (2, -3) and B is (1, 4).
If a vertex of a triangle be (1, 1) and the middle points of the sides through it be (-2,-3) and (5 2) find the other vertices.
Show that the mid-point of the line segment joining the points (5, 7) and (3, 9) is also the mid-point of the line segment joining the points (8, 6) and (0, 10).
Find the ratio in which the join of (–4, 7) and (3, 0) is divided by the y-axis. Also, find the co-ordinates of the point of intersection.
Find the co-ordinates of the points of tri-section of the line joining the points (–3, 0) and (6, 6).
If A = (−4, 3) and B = (8, −6)
- Find the length of AB.
- In what ratio is the line joining A and B, divided by the x-axis?
A line segment joining A`(-1,5/3)` and B(a, 5) is divided in the ratio 1 : 3 at P, the point where the line segment AB intersects the y-axis.
- Calculate the value of ‘a’.
- Calculate the co-ordinates of ‘P’.
AB is a diameter of a circle with centre C = (–2, 5). If A = (3, –7), find
- the length of radius AC.
- the coordinates of B.
M and N are two points on the X axis and Y axis respectively. P (3, 2) divides the line segment MN in the ratio 2 : 3.
Find:
(i) the coordinates of M and N
(ii) slope of the line MN.
Find the coordinate of a point P which divides the line segment joining :
A(-8, -5) and B (7, 10) in the ratio 2:3.
Find the ratio in which the line x = -2 divides the line segment joining (-6, -1) and (1, 6). Find the coordinates of the point of intersection.
The origin o (0, O), P (-6, 9) and Q (12, -3) are vertices of triangle OPQ. Point M divides OP in the ratio 1: 2 and point N divides OQ in the ratio 1: 2. Find the coordinates of points M and N. Also, show that 3MN = PQ.
In what ratio does the x-axis divide the line segment joining the points (– 4, – 6) and (–1, 7)? Find the coordinates of the point of division.
