Advertisements
Advertisements
प्रश्न
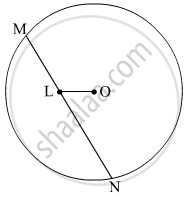
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
उत्तर
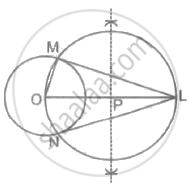
Steps of construction:
- Draw a circle with an O in the centre and a radius of 3 cm.
- Line the outside of the circle with a point so that OL = 7 cm.
- Make a perpendicular bisector of OL segment. It crosses OL at P.
- Draw another circle overlapping the given circle at points M and N, with Pas as the centre and radius equal to PL.
- Join with LM and LN.
Tangents to the circle are segments LM and LN.
Justification: If we join O and M, then
∠OML = 90° ......[Angle in a semi-circle]
So, LM ⊥ OM
The radius of the circle is shown by OM in the figure.
Therefore, from point L, LM is a tangent to the circle.
Similarly, from point L, LN is a tangent to the circle.
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

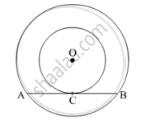
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
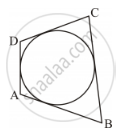
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
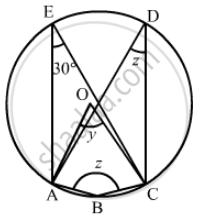
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.


In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
State, if the following statement is true or false:
If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
In figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR = 70° and (arc RS) = 80°, find
(i) m(arc PR)
(ii) m(arc QS)
(iii) m(arc QSR)
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
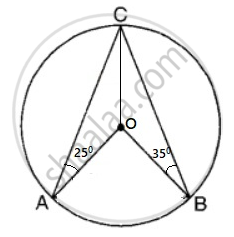
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.