Advertisements
Advertisements
प्रश्न
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
उत्तर

Here, T, S and U are the points of contact of the circle with the sides QR, PQ and PR, respectively.
OT = OS = OU = 8 cm (Radii of the circle)
We know that the lengths of tangents drawn from an external point to a circle are equal.
∴ QS = QT = 14 cm
RU = RT = 16 cm
PS = PU = x cm (say)
So, QR = QT + TR = 14 cm + 16 cm = 30 cm
PQ = PS + SQ = x cm + 14 cm = (x + 14) cm
PR = PU + UR = x cm + 16 cm = (x + 16) cm
Also, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OT ⊥ QR, OS ⊥ PQ and OU ⊥ PR
Now,
ar(∆OQR) + ar(∆OPQ) + ar(∆OPR) = ar(∆PQR)
\[\therefore \frac{1}{2} \times QR \times OT + \frac{1}{2} \times PQ \times OS + \frac{1}{2} \times PR \times OU = 336 {cm}^2 \]
\[ \Rightarrow \frac{1}{2} \times 30 \times 8 + \frac{1}{2} \times \left( x + 14 \right) \times 8 + \frac{1}{2} \times \left( x + 16 \right) \times 8 = 336\]
\[ \Rightarrow 120 + 4x + 56 + 4x + 64 = 336\]
\[ \Rightarrow 8x + 240 = 336\]
\[\Rightarrow 8x = 336 - 240 = 96\]
\[ \Rightarrow x = 12\]
∴ PQ = (x + 14) cm = (12 + 14) cm = 26 cm
PR = (x + 16) cm = (12 + 16) cm = 28 cm
Hence, the lengths of sides PQ and PR are 26 cm and 28 cm, respectively.
APPEARS IN
संबंधित प्रश्न
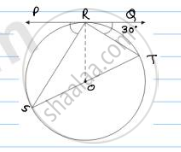
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal ?
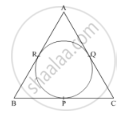
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
In the figure, O is the centre of a circle, AB is a chord, and AT is the tangent at A. If ∠AOB = 100°, then ∠BAT is equal to ______

If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
Find the length of the arc of a circle which subtends an angle of 60° at the centre of the circle of radius 42 cm.
