Advertisements
Advertisements
प्रश्न
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
उत्तर

Here, T, S and U are the points of contact of the circle with the sides QR, PQ and PR, respectively.
OT = OS = OU = 8 cm (Radii of the circle)
We know that the lengths of tangents drawn from an external point to a circle are equal.
∴ QS = QT = 14 cm
RU = RT = 16 cm
PS = PU = x cm (say)
So, QR = QT + TR = 14 cm + 16 cm = 30 cm
PQ = PS + SQ = x cm + 14 cm = (x + 14) cm
PR = PU + UR = x cm + 16 cm = (x + 16) cm
Also, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OT ⊥ QR, OS ⊥ PQ and OU ⊥ PR
Now,
ar(∆OQR) + ar(∆OPQ) + ar(∆OPR) = ar(∆PQR)
\[\therefore \frac{1}{2} \times QR \times OT + \frac{1}{2} \times PQ \times OS + \frac{1}{2} \times PR \times OU = 336 {cm}^2 \]
\[ \Rightarrow \frac{1}{2} \times 30 \times 8 + \frac{1}{2} \times \left( x + 14 \right) \times 8 + \frac{1}{2} \times \left( x + 16 \right) \times 8 = 336\]
\[ \Rightarrow 120 + 4x + 56 + 4x + 64 = 336\]
\[ \Rightarrow 8x + 240 = 336\]
\[\Rightarrow 8x = 336 - 240 = 96\]
\[ \Rightarrow x = 12\]
∴ PQ = (x + 14) cm = (12 + 14) cm = 26 cm
PR = (x + 16) cm = (12 + 16) cm = 28 cm
Hence, the lengths of sides PQ and PR are 26 cm and 28 cm, respectively.
APPEARS IN
संबंधित प्रश्न
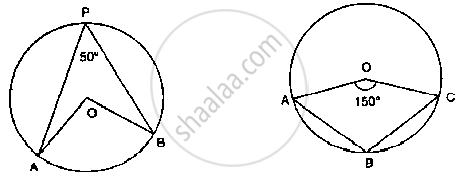
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
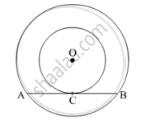
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.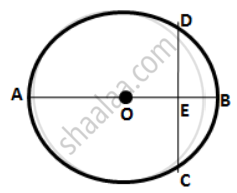
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

Use the figure given below to fill in the blank:
Diameter = 2 x ________

Draw circle with diameter: 8.4 cm
In above case, measure the length of the radius of the circle drawn.
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
In the given figure, O is the centre of the circle. Name a chord, which is not the diameter of the circle.