Advertisements
Advertisements
प्रश्न
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure
उत्तर
Here, AB is a diameter of the circle from point C and a tangent is drawn which meets at a point P.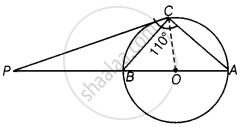
Join OC.
Here, OC is radius.
Since, tangent at any point of a circle is perpendicular to the radius through point of contact circle.
∴ OC ⊥ PC
Now, ∠PCA = 110° ...[Given]
⇒ ∠PCO + ∠OCA = 110°
⇒ 90° + ∠OCA = 110°
⇒ ∠OCA = 20°
∴ OC = OA = Radius of circle
⇒ ∠OCA = ∠OAC = 20° ...[Since, two sides are equal, then their opposite angles are equal]
Since, PC is a tangent,
So ∠BCP = ∠CAB = 20° ...[Angles in a alternate segment are equal]
In ΔPBC,
∠P + ∠C + ∠A = 180°
∠P = 180° – (∠C + ∠A)
= 180° – (110° + 20°)
= 180° – 130°
= 50°
In ΔPBC,
∠BPC + ∠PCB + ∠PBC = 180° ...[Sum of all interior angles of any triangle is 180°]
⇒ 50° + 20° + ∠PBC = 180°
⇒ ∠PBC = 180° – 70°
⇒ ∠PBC = 110°
Since, APB is a straight line.
∴ ∠PBC + ∠CBA = 180°
⇒ ∠CBA = 180° – 110° = 70°
संबंधित प्रश्न
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
State, if the following statement is true or false:
The diameters of a circle always pass through the same point in the circle.
Twice the radius is ________________
Find the length of the arc of a circle which subtends an angle of 60° at the centre of the circle of radius 42 cm.
AB is a chord of a circle with centre O. AOC is diameter of circle, AT is a tangent at A.
Write answers of the following questions:
- Draw the figure using the given information.
- Find the measures of ∠CAT and ∠ABC with reasons.
- Whether ∠CAT and ∠ABC are congruent? Justify your answer.
