Advertisements
Advertisements
प्रश्न
In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.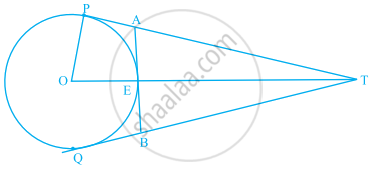
उत्तर
Given: A circle with center O and radius = 5 cm T is a point, OT = 13 cm. OT intersects the circle at E and AB is the tangent to the circle at E.
To Find: Length of AB
OP ⊥ PT ...[Tangent at a point on the circle is perpendicular to the radius through point of contact]
By pythagoras theorem in ∆OPT right angled at P
(OT)2 = (OP)2 + (PT)2
(13)2 = (5)2 + (PT)2
(PT)2 = 169 – 25 = 144
PT = 12 cm
PT = TQ = 12 cm ...[Tangents drawn from an external point to a circle are equal]
Now, OT = OE + ET
ET = OT – OE
= 13 – 5
= 8 cm
Now, as Tangents drawn from an external point to a circle are equal.
AE = PA ...[1]
EB = BQ ...[2]
Also OE ⊥ AB ...[Tangent at a point on the circle is perpendicular to the radius through point of contact]
∠AEO = 90°
∠AEO + ∠AET = 180° ...[By linear Pair]
∠AET = 90°
In ΔAET By Pythagoras Theorem
(AT)2 = (AE)2 + (ET)2 ...[Here AE = PA as tangents drawn from an external point to a circle are equal]
(PT – PA)2 = (PA)2 + (ET)2
(12 – PA)2 = (PA)2 + (8)2 ...[From 1]
144 + (PA)2 – 24PA = (PA)2 + 64
24PA = 80 ...[3]
∠AET + ∠BET = 180° ...[Linear Pair]
90° + ∠BET = 180°
∠BET = 90°
In ΔBET, By Pythagoras Theorem
(BT)2 = (BE)2 + (ET)2
(TQ – BQ)2 = (BQ)2 + (ET)2 ...[From 2]
(12 – BQ)2 = (BQ)2 + (8)2
144 + (BQ)2 – 24BQ = (BQ)2 + 64
24BQ = 80 ...[4]
So, AB = AE + BE
AB = PA + BQ ...[From 1 and 2]
AB = `10/3 + 10/3` ...[From 3 and 4]
AB = `20/3` cm
APPEARS IN
संबंधित प्रश्न
A tangent to a circle intersects it in ______ point (s).
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

In the given figure, find TP if AT = 16 cm and AB = 12 cm.

In the given figure AC is a tangent to the circle with centre O.
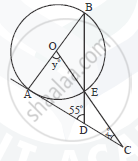
If ∠ADB = 55° , find x and y. Give reasons for your answers.
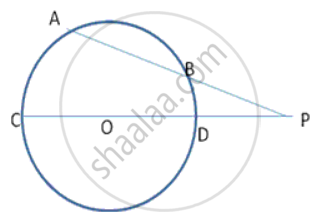
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
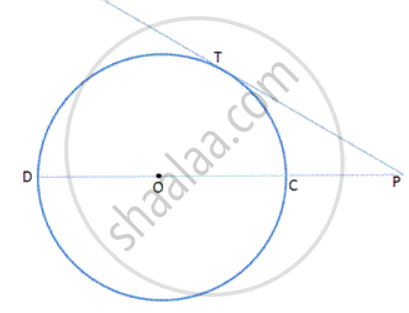
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
Two parallel lines touch the circle at
points A and B respectively. If the area of the circle is 25 n cm2, then AB is equal to ______
A: What is a line called, if it meets the circle at only one point?
B: Collection of all points equidistant from a fixed point is ______.
- Chord
- Tangent
- Circle
- Curve
- Secant
Which is correct matching?
ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
