Advertisements
Advertisements
प्रश्न
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
उत्तर
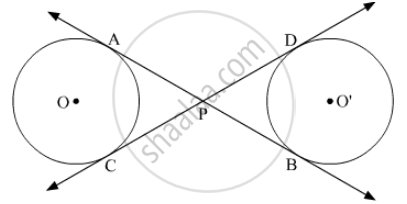
Given: Two circles with centre’s O and O'. AB and CD are common tangents to the circles which intersect in P.
To Prove: AB = CD
Proof:
AP = PC (length of tangents drawn from an external point to the circle are equal) ..… (1)
PB = PD (length of tangents drawn from an external point to the circle are equal) ..… (2)
Adding (1) and (2), we get
AP + PB = PC + PD
⇒ AB = CD
Hence Proved
APPEARS IN
संबंधित प्रश्न
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

Use the figure given below to fill in the blank:
Diameter of a circle is ______.

In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
Is every diameter of a circle also a chord?
