Advertisements
Advertisements
प्रश्न
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

उत्तर

Given: AB and CD are common tangents to both the circles.
To prove: AB = CD
Proof:
We know that two tangents drawn to a circle for the same exterior point are
equal.
Thus we get
AE = EC (i)
Similarly
ED = EB (ii)
AB = AE + EB (iii)
and
CD = CE + ED (iv)
AB = EC + EB from (i) and (iii)
CD = EC + EB from (ii) and (iv)
Therefore AB = CD
Hence proved.
APPEARS IN
संबंधित प्रश्न
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.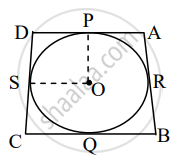
A line through the point of contact and passing through centre of the circle is known as ______
In the adjoining figure, Δ ABC is circumscribing a circle. Then, the length of BC is ______