Advertisements
Advertisements
प्रश्न
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

उत्तर
We know that tangent segments to a circle from the same external point are congruent
Now, we have
AR = AO, BR = BP and CP = CQ
Now, AB = AC
⇒ AR+ RB= AQ+ QC
⇒ AR + RB = AR + OC
⇒ RB = QC
⇒ BP = CP
Hence, P bisects BC at P.
संबंधित प्रश्न
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
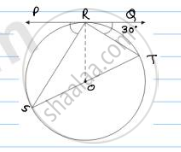
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
The length of three concesutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
A point P is 10 cm from the center of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to ______
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

In the given figure, O is the centre of the circle. Name all chords of the circle.