Advertisements
Advertisements
Question
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

Solution
We know that tangent segments to a circle from the same external point are congruent
Now, we have
AR = AO, BR = BP and CP = CQ
Now, AB = AC
⇒ AR+ RB= AQ+ QC
⇒ AR + RB = AR + OC
⇒ RB = QC
⇒ BP = CP
Hence, P bisects BC at P.
RELATED QUESTIONS
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
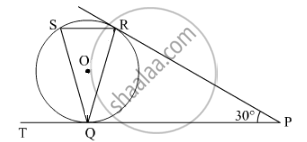
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
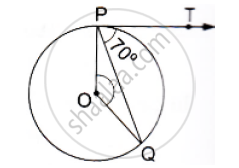
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

Use the figure given below to fill in the blank:
Tangent to a circle is _______.

Use the figure given below to fill in the blank:
If the length of RS is 5 cm, the length of PQ = _______

Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
Find the radius of the circle
Diameter = 76 cm
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
From the figure, identify two points in the interior.

