Advertisements
Advertisements
Question
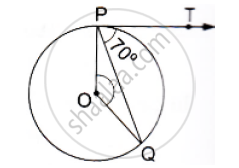
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
Solution
We know that the radius and tangent are perpendicular at their point of contact.
∴ ∠OPT = 90°
Now, ∠OPQ = ∠OPT - ∠TPQ = 90° -70° = 20°
Since, OP = OQ as both are radius
∴ ∠OPQ = ∠OQP = 20° (Angles opposite to equal sides are equal)
Now, In isosceles Δ POQ
∠POQ + ∠OPQ + ∠OQP = 180° (Angle sum property of a triangle)
⇒ ∠POQ =180° - 20° = 140°
APPEARS IN
RELATED QUESTIONS
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
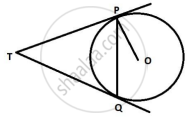
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

In the given circle with diameter AB, find the value of x.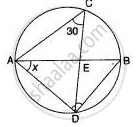
Draw circle with the radii given below.
2 cm
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is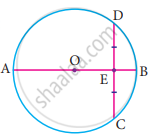
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

If a number of circles pass through the endpoints P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

