Advertisements
Advertisements
प्रश्न
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
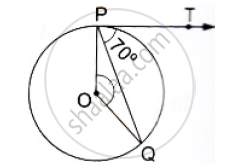
उत्तर
We know that the radius and tangent are perpendicular at their point of contact.
∴ ∠OPT = 90°
Now, ∠OPQ = ∠OPT - ∠TPQ = 90° -70° = 20°
Since, OP = OQ as both are radius
∴ ∠OPQ = ∠OQP = 20° (Angles opposite to equal sides are equal)
Now, In isosceles Δ POQ
∠POQ + ∠OPQ + ∠OQP = 180° (Angle sum property of a triangle)
⇒ ∠POQ =180° - 20° = 140°
APPEARS IN
संबंधित प्रश्न
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
In the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects PQ at A and RS at B. Prove that ∠AOB = 90º
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of another chord.
Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
Can the length of a chord of a circle be greater than its diameter ? Explain.
Find the radius of the circle
Diameter = 76 cm
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
AB is a chord of a circle with centre O. AOC is diameter of circle, AT is a tangent at A.
Write answers of the following questions:
- Draw the figure using the given information.
- Find the measures of ∠CAT and ∠ABC with reasons.
- Whether ∠CAT and ∠ABC are congruent? Justify your answer.
