Advertisements
Advertisements
Question
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is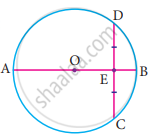
Options
8 cm
4 cm
6 cm
10 cm
Solution
10 cm
Explanation;
Hint: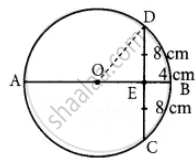
Let the radius OD be x.
OE = OB – BE
= x – 4 ...(OB radius of the circle)
In the ΔOED,
OD2 = OE2 + ED2
x2 = (x – 4)2 + 82
x2 = x2 + 16 – 8x + 64
8x = 80
x = `80/8`
= 10 cm
Radius of the circle = 10 cm.
APPEARS IN
RELATED QUESTIONS
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
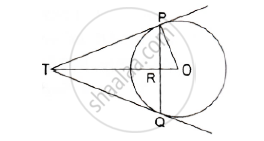
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
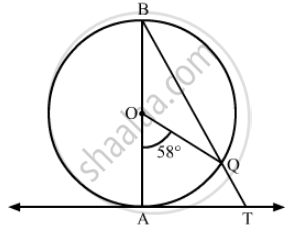
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
State, if the following statement is true or false:
The longest chord of a circle is its diameter.
A line segment with its end points on the circle is called a ______________
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
