Question

The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.

Answer 1

Let ABC be the triangle whose circumcenter is O.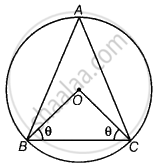

∠OBC = ∠OCB = θ  ...(Opposite angles of equal sides)

In ΔBOC, using the angle sum property of tringle, sum of all angles is 180°, we have:

∠BOC + ∠OBC + ∠OCB = 180°

⇒ ∠BOC + θ + θ = 180°

⇒ ∠BOC = 180° – 2θ

Also, in a circle, angle subtended by an arc at the center is twice the angle subtended by it at any other point in the remaining part of the circle.

∠BOC = 2∠BAC

⇒ ∠BAC = `1/2`(∠BOC)

⇒ ∠BAC = `1/2`(180° – 2θ)

⇒ ∠BAC = (90° – θ)

⇒ ∠BAC + θ = 90°

⇒ ∠BAC + ∠OBC = 90°

Hence proved.