Advertisements
Advertisements
Question
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
Solution

Given: Chord AB || tangent XY
AB = `16sqrt(3)` units
PQ is radius of the circle.
PC = CQ
To find: Radius of the circle, i.e., l(PQ)
Construction: Draw seg PB.
In given figure, ∠PQY = 90° ......(i) [Tangent theorem]
Chord AB || line XY .....[Given]
∴ ∠PCB ≅ ∠PQY .....[Corresponding angles]
∴ ∠PCB = 90° .....(ii) [From (i)]
Now CB = `1/2` AB
∴ CB = `1/2 xx 16sqrt(3)` .....`[("A perpendicular drawn from the"),("centre of a circle on its chord"),("bisects the chord")]`
CB = `8sqrt(3)` units .....(iii)
Let the radius of the circle be x units .....(iv)
∴ PQ = x
∴ `"PC" = 1/2 "PQ"` ........[PC = CQ, P–C–Q]
∴ `"PC" = 1/2 x` .......(v)
In ∆PCB,
∠PCB = 90° .....[From (ii)]
∴ PB2 = PC2 + CB2 .....[Pythagoras theorem]
∴ x2 = `(1/2 x)^2 + (8sqrt(3))^2` .....[From (iii), (iv) and (v)]
∴ x2 = `x^2/4 + 64 xx 3`
∴ 4x2 = `(x^2)/4 + 192`
∴ `(4x^2 – x^2)/4` = 192
∴ `(3x^2)/4` = 192
∴ x2 = `192/3 xx 4`
∴ x2 = 256
∴ `sqrt(x^2)` = `sqrt256`
∴ x = 16 units ......[Taking square root of both sides]
∴ The radius of the circle is 16 units.
APPEARS IN
RELATED QUESTIONS
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
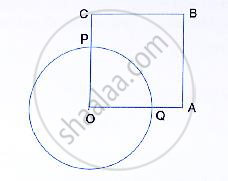
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

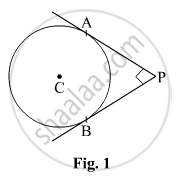
In Fig. 1, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then the length of each tangent is:
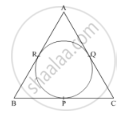
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
The circumference of a circle is 22 cm. The area of its quadrant (in cm2) is
In the given figure, OQ : PQ = 3.4 and perimeter of Δ POQ = 60 cm. Determine PQ, QR and OP.
The circle which passes through all the vertices of a triangle is called ______.
Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is ______.
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
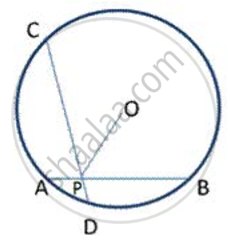

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 15 cm |
Twice the radius is ________________
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]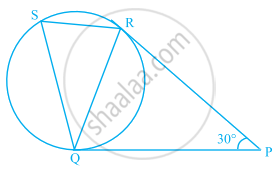
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

