Advertisements
Advertisements
Question
Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is ______.
Options
12 cm
13 cm
14 cm
15 cm
Solution
Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is 13 cm.
Explanation:
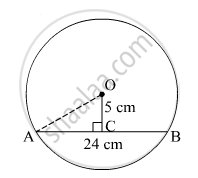
Let the chord be AB = 24 cm
Distance of the chord from the centre O is 5 cm.
AO is the radius of the circle.
Perpendicular from the centre of the circle to the chord bisects the chord.
So, AC = CB
In ΔAOC,
OC2 + AC2 = AO2
⇒ 52 + 122 = AO2
⇒ AO2 = 25 + 144
⇒ AO2 = 169
⇒ AO = 13 cm
Thus, the radius of the circle is 13 cm.
APPEARS IN
RELATED QUESTIONS
In the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects PQ at A and RS at B. Prove that ∠AOB = 90º
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
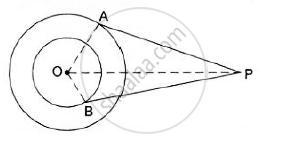
In the given figure, O is the centre of the two concentric circles of radii 4 cm and 6cm respectively. AP and PB are tangents to the outer and inner circle respectively. If PA = 10cm, find the length of PB up to one place of the decimal.
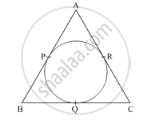
In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.
If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is ______
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

