Advertisements
Advertisements
Question
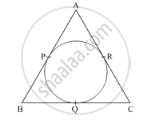
In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
Options
A. 11
B. 10
C. 14
D. 15
Solution
Given, AP = 4 cm, BP = 3 cm and AC = 11 cm.
The lengths of tangents drawn from an external point to the circle are equal.
AP = AR, BP = BQ, CQ = CR …….. (1)
AC = 11 cm
⇒ AR + RC = 11 cm
⇒ AP + CQ = 11 cm [From equation (1)]
⇒ 4 cm + CQ = 11 cm
⇒ CQ = (11 − 4) cm
⇒ CQ = 7 cm
BP = BQ = 3 cm
Now, BC = BQ + QC
⇒ BC = (3 + 7) cm
⇒ BC = 10 cm
Hence, the correct option is B.
APPEARS IN
RELATED QUESTIONS
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

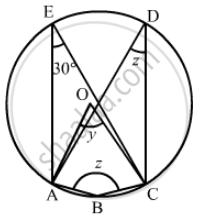
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
A line segment with its end points on the circle is called a ______________
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
