Advertisements
Advertisements
प्रश्न
Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is ______.
विकल्प
12 cm
13 cm
14 cm
15 cm
उत्तर
Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is 13 cm.
Explanation:
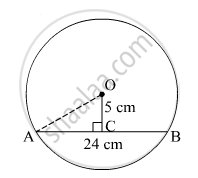
Let the chord be AB = 24 cm
Distance of the chord from the centre O is 5 cm.
AO is the radius of the circle.
Perpendicular from the centre of the circle to the chord bisects the chord.
So, AC = CB
In ΔAOC,
OC2 + AC2 = AO2
⇒ 52 + 122 = AO2
⇒ AO2 = 25 + 144
⇒ AO2 = 169
⇒ AO = 13 cm
Thus, the radius of the circle is 13 cm.
APPEARS IN
संबंधित प्रश्न
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Use the figure given below to fill in the blank:
If the length of RS is 5 cm, the length of PQ = _______

State, if the following statement is true or false:
The longest chord of a circle is its diameter.
Draw circle with the radii given below.
4 cm
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.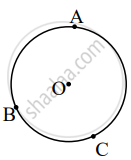
From the figure, identify three radii.
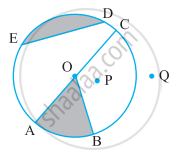
From the figure, identify a sector.

If radius of a circle is 5 cm, then find the length of longest chord of a circle.
