Advertisements
Advertisements
प्रश्न
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
उत्तर

Given: Chord AB || tangent XY
AB = `16sqrt(3)` units
PQ is radius of the circle.
PC = CQ
To find: Radius of the circle, i.e., l(PQ)
Construction: Draw seg PB.
In given figure, ∠PQY = 90° ......(i) [Tangent theorem]
Chord AB || line XY .....[Given]
∴ ∠PCB ≅ ∠PQY .....[Corresponding angles]
∴ ∠PCB = 90° .....(ii) [From (i)]
Now CB = `1/2` AB
∴ CB = `1/2 xx 16sqrt(3)` .....`[("A perpendicular drawn from the"),("centre of a circle on its chord"),("bisects the chord")]`
CB = `8sqrt(3)` units .....(iii)
Let the radius of the circle be x units .....(iv)
∴ PQ = x
∴ `"PC" = 1/2 "PQ"` ........[PC = CQ, P–C–Q]
∴ `"PC" = 1/2 x` .......(v)
In ∆PCB,
∠PCB = 90° .....[From (ii)]
∴ PB2 = PC2 + CB2 .....[Pythagoras theorem]
∴ x2 = `(1/2 x)^2 + (8sqrt(3))^2` .....[From (iii), (iv) and (v)]
∴ x2 = `x^2/4 + 64 xx 3`
∴ 4x2 = `(x^2)/4 + 192`
∴ `(4x^2 – x^2)/4` = 192
∴ `(3x^2)/4` = 192
∴ x2 = `192/3 xx 4`
∴ x2 = 256
∴ `sqrt(x^2)` = `sqrt256`
∴ x = 16 units ......[Taking square root of both sides]
∴ The radius of the circle is 16 units.
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
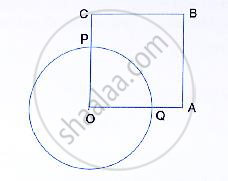
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
Use the figure given below to fill in the blank:
AB is a ______ of the circle.

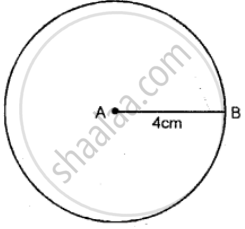
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
State, if the following statement is true or false:
The longest chord of a circle is its diameter.
The ratio between the circumference and diameter of any circle is _______
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
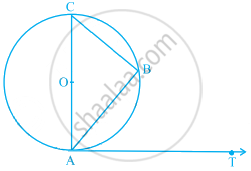
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
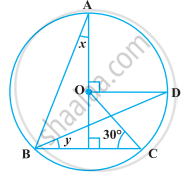
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
In the given figure, O is the centre of the circle. Name a chord, which is not the diameter of the circle.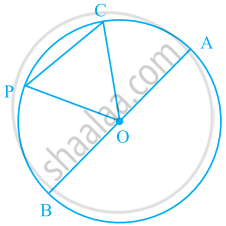
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.