Advertisements
Advertisements
प्रश्न
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
उत्तर
It is given that, AB as diameter, O is centre and`angle CAB = 30°`
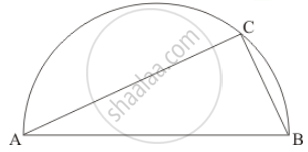
We have to find `m angleACB` and ` m angleABC`
Since angle in a semi-circle is a right angle therefore
`angleACB = 90°`
In Δ ACD we have
`angleCAB` = 30° (Given)
`angleACB `= 90° (Angle in semi-circle is right angle)
Now in Δ ACB we have
`angleCAB + angleACB + angleABC `= 180
`angleABC = 180° - (angle CAB + angleCAB )`
=180° - (90° + 30° )
= 180° - 120°
= 60°
Hence `angle ABC = 60°` and `angleACB = 90°`
APPEARS IN
संबंधित प्रश्न
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
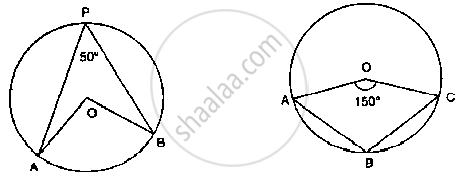
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
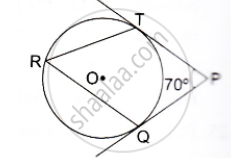
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
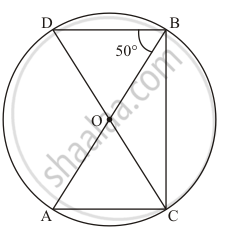
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
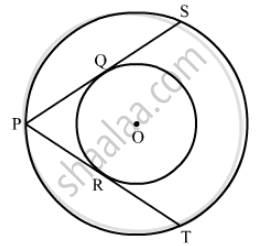
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
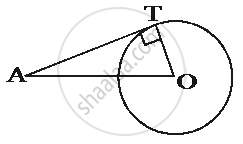
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
Find the length of the arc of a circle which subtends an angle of 60° at the centre of the circle of radius 42 cm.
If an are subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is ______.
