Advertisements
Advertisements
Question
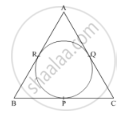
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
Solution
Given: An isosceles ΔABC with AB = AC, circumscribing a circle.
To prove: P bisects BC
Proof: AR and AQ are the tangents drawn from an external point A to the circle.
∴ AR = AQ (Tangents drawn from an external point to the circle are equal)
Similarly, BR = BP and CP = CQ.
It is given that in ΔABC, AB = AC.
⇒ AR + RB = AQ + QC
⇒ BR = QC (As AR = AQ)
⇒ BP = CP (As BR = BP and CP = CQ)
⇒ P bisects BC
Hence, the result is proved.
APPEARS IN
RELATED QUESTIONS
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
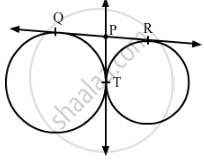
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
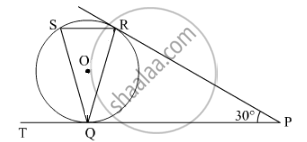
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
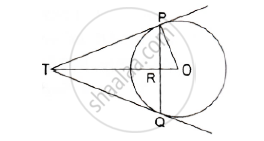
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

Two concentric circles with center O have A, B, C, D as the points of intersection with the lines L shown in the figure. If AD = 12 cm and BC s = 8 cm, find the lengths of AB, CD, AC and BD.
A point P is 10 cm from the center of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to ______
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
