Advertisements
Advertisements
Question
Two concentric circles with center O have A, B, C, D as the points of intersection with the lines L shown in the figure. If AD = 12 cm and BC s = 8 cm, find the lengths of AB, CD, AC and BD.
Solution
Since, OM ⊥ BC
BM = CM = `1/2`BC = 4 cm
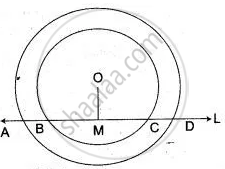
also, OM ⊥ AD
So, AM = DM = `1/2` AD = 6 cm
now, AB = AM - BM = ( 6 - 4 ) cm = 2 cm
CD = DM - CM = ( 6 - 4 ) cm = 2 cm
∴ AC = AB + BC = ( 2 + 8 ) cm = 10 cm
and BD = BC + CD = ( 8 + 2 ) cm = 10 cm
APPEARS IN
RELATED QUESTIONS
In fig., O is the centre of the circle, PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic.
Prove that two different circles cannot intersect each other at more than two points.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

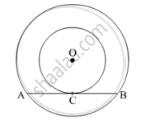
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

Find the length of the arc of a circle which subtends an angle of 60° at the centre of the circle of radius 42 cm.
