Advertisements
Advertisements
Question
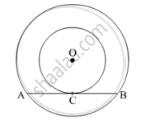
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
Solution
Given: Two concentric circles C1 and C2 with centre O, and AB is the chord of C1 touching C2 at C.
To prove: AC = CB
Construction: Join OC.
Proof: AB is the chord of C1 touching C2 at C, then AB is the tangent to C2 at C with OC as its radius.
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OC ⊥ AB
Considering, AB as the chord of the circle C1. So, OC ⊥ AB.
∴ OC is the bisector of the chord AB.
Hence, AC = CB (Perpendicular from the centre to the chord bisects the chord).
APPEARS IN
RELATED QUESTIONS
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
One chord of a circle is known to be 10 cm. The radius of this circle must be
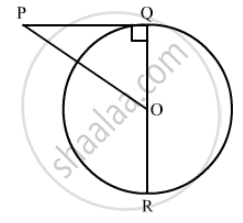
In the given figure, OQ : PQ = 3.4 and perimeter of Δ POQ = 60 cm. Determine PQ, QR and OP.
If O is the centre of the circle, find the value of x in each of the following figures

The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
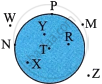
In the table below, write the names of the points in the interior and exterior of the circle and those on the circle.
| Diagram | Points in the interior of the circle |
Points in the exterior of the circle |
Points on the circle |
 |
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

From the figure, identify a chord.

