Advertisements
Advertisements
Question
Prove that two different circles cannot intersect each other at more than two points.
Solution
Suppose two circles intersect in three points A,B,C,
Then A,B,C are non-collinear. So, a unique circle passes through these three points. This is contradiction to the face that two given circles are passing through A,B,C. Hence, two circles cannot intersect each other at more than two points.
APPEARS IN
RELATED QUESTIONS
In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
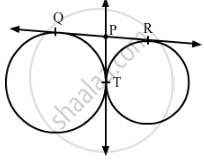
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
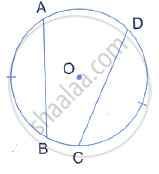
A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal ?
Two concentric circles are of diameters 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
If O is the centre of the circle, find the value of x in each of the following figures
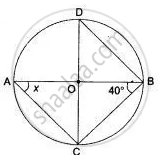
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

