Advertisements
Advertisements
Question
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
Advertisements
Solution
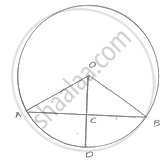
Given: C is the midpoint of chord AB
To prove: D is the midpoint of arc AB Proof:∠
In Δ OAC and ΔOBC
OA=OB [Radius of circle]
OC=OC [Common]
AC=BC [C is the midpoint of AB]
Then, ΔOAC = ΔOBC [By SSS condition]
`∴∠AOC=∠BOC` [ c. p.c.t ]
`⇒m(AD)=M(BD)`
`⇒AD≅ BD `
Here ,D is the midpoint of arc AB
APPEARS IN
RELATED QUESTIONS
In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
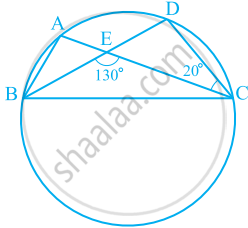
In the given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
Fill in the blank:
A circle divides the plane, on which it lies, in ............ parts.
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
Given an arc of a circle, show how to complete the circle.
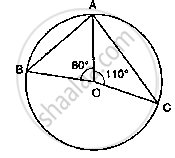
In the below fig. O is the centre of the circle. Find ∠BAC.
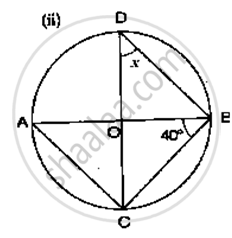
If O is the centre of the circle, find the value of x in the following figure
In the given figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.
Prove that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half the hypotenuse.
A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
